File:CX SPHERE.png

原始文件 (3,282 × 2,216像素,文件大小:736 KB,MIME类型:image/png)
摘要
| 描述CX SPHERE.png |
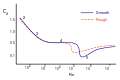
Français : Cx de la sphère lisse selon son Reynolds diamétral ; Cx des balles de golf, de tennis et de football ; Cx des sphères rugueuses selon Achenbach ;Cx des gouttes de pluie et de brouillard selon leur diamètre équivalent. Définition du Cx. |
| 日期 | |
| 来源 | 自己的作品 |
| 作者 | Bernard de Go Mars |
| 其他版本 |
[编辑] .svg:
.png:
.jpg:
|
许可协议
- 您可以自由地:
- 共享 – 复制、发行并传播本作品
- 修改 – 改编作品
- 惟须遵守下列条件:
- 署名 – 您必须对作品进行署名,提供授权条款的链接,并说明是否对原始内容进行了更改。您可以用任何合理的方式来署名,但不得以任何方式表明许可人认可您或您的使用。
- 相同方式共享 – 如果您再混合、转换或者基于本作品进行创作,您必须以与原先许可协议相同或相兼容的许可协议分发您贡献的作品。
| 注解 InfoField | 该图片含有注解:在维基媒体共享资源上查看注解 |
Compilation et tracé des courbes par Bernard de Go Mars. Mise en page par AERODYNE.
Le comportement de la balle de tennis est tout à fait particulier ; les mécaniciens des fluides considèrent que la rugosité due à ses poils place cette balle, de façon très anticipée, en régime post-critique, c-à-d dans le régime existant, pour les sphères lisses, après le super-critique... La légère diminution du Cx quand le Reynolds augmente est attribué à la flexion des poils de feutre sous l'effet de la Traînée aérodynamique.
Comme on le sait, les alvéoles présentes à la surface de la balle de golf déclenchent, de façon anticipée, la transition de la couche limite depuis son régime laminaire jusqu'à son régime turbulent.
C'est cette "crise du Cx" de la balle de football qui permet aux joueurs d'obtenir, avec utilisation de l'effet Magnus-Robin, des trajectoires pouvant tromper les gardiens de but.
Dans tout ce graphe, le Cx est établi en référence à la surface frontale de la sphère et au carré de la vitesse du fluide. Dans la partie gauche de la courbe rouge, en régime de Stokes (ou assimilé), la Traînée devient proportionnelle à la vitesse (et non plus au carré de la vitesse) : le Cx, tel qu'il est donné par la courbe rouge de ce graphe, n'a donc plus de signification physique mais il garde néanmoins sa réalité numérique : il permet toujours de calculer la Traînée ; pour obtenir cette Traînée, il suffit de multiplier ledit Cx par la moitié de la Masse Volumique, par le carré de la vitesse et par la surface frontale de la sphère...
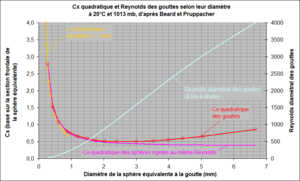
Les gouttes de brouillards tombent tellement lentement qu'on peut penser qu'elles flottent dans l'air ; il n'en est rien : Elles tombent, comme les gouttes de pluie, à une vitesse où l'équilibre se fait entre leur poids et leur Traînée aérodynamique. Noter que le Cx des petites gouttes de brouillard est très fort. Pour les grosses gouttes de pluie, dont la forme n'est plus sphérique (elles sont aplaties, voire creusées, à leur point d'arrêt par la Pression Dynamique), le diamètre indiqué est le diamètre équivalent, c-à-d celui d'une goutte parfaitement sphérique qui aurait la même masse.
La courbe rouge est nommée "courbe standard". Dans leur ouvrage BUBBLES, DROPS, AND PARTICLES, 1978, Academic Press, Clift, Grace et Weber donnent les équations permettant de la dessiner tronçon par tronçon.
En régime de Stokes, la Traînée est proportionnelle à la vitesse et non plus au carré de la vitesse. Ceci étant, le Cx donné par la courbe rouge (ou "courbe standard"), s'il n'a plus de signification physique, reste tout à fait valide : il permet toujours, en effet, de calculer la Traînée : pour obtenir cette Traînée, il suffit de multiplier ledit Cx par la moitié de la Masse Volumique, par le carré de la vitesse et par la surface frontale de la sphère...
Les rugosités relatives étudiées par Achenbach sont, de la gauche vers la droite :
1250 10^-5,
500 10^-5,
150 10^-5 et
25 10^-5.
La rugosité relative est définie comme le quotient de la hauteur moyenne des aspérités (depuis les sommets jusqu’au fond des creux) par la dimension caractéristique du corps (ici son diamètre).
Compilation et tracé des courbes par Bernard de Go Mars. Mise en page par AERODYNE.
Le comportement de la balle de tennis est tout à fait particulier ; les mécaniciens des fluides considèrent que la rugosité due à ses poils place cette balle,de façon très anticipée, en régime hyper-critique, c-à-d dans le régime existant, pour les sphères lisses, après le super-critique...
La légère diminution du Cx quand le Reynolds augmente est attribué à la flexion des poils de feutre sous l'effet de la Traînée aérodynamique.
Comme on le sait, les alvéoles présentes à la surface de la balle de golf déclenchent, de façon anticipée, la transition de la couche limite depuis son régime laminaire jusqu'à son régime turbulent. C'est ce qui diminue notablement leur 
C'est cette "crise du Cx" de la balle de football qui permet aux joueurs, avec utilisation de l'effet Magnus-Robin, d'obtenir des trajectoires pouvant tromper les gardiens de but.
Les gouttes de brouillards tombent tellement lentement qu'on peut penser qu'elles flottent dans l'air : il n'en est rien. Elles tombent, comme les gouttes de pluie, à une vitesse où l'équilibre se fait entre leur poids et leur Traînée aérodynamique.
Noter que le 

Pour les grosses gouttes de pluie, dont la forme n'est plus sphérique (elles sont aplaties, voire creusées, à leur point d'arrêt par la Pression Dynamique), le diamètre indiqué est le diamètre équivalent, c-à-d celui d'une goutte parfaitement sphérique qui aurait le même volume.
Du fait que les grosses gouttes de pluie sont déformées par les efforts aérodynamiques, leur 
Pour ce problème de la vitesse des gouttes d'eau, voir les graphes :
La courbe rouge est nommée "courbe standard". Dans leur ouvrage "BUBBLES, DROPS, AND PARTICLES", Academic Press, 1978, [1], Clift, Grace et Weber donnent les équations permettant de la dessiner tronçon par tronçon.
En régime de Stokes, la Traînée est proportionnelle à la vitesse et non plus au carré de la vitesse, ainsi que proportionnelle à une longueur caractéristique (le diamètre, par exemple, pour la sphère) et non plus à la surface frontale.
Ceci étant, le 

Dans tout ce graphe, le 

Dans la partie gauche de la courbe rouge, en régime de Stokes (ou assimilé), la Traînée devient proportionnelle à la vitesse (et non plus au carré de la vitesse) ainsi que proportionnelle à une longueur caractéristique du corps (le diamètre, par exemple, pour la sphère) : le 

Lorsque les gouttes d’eau grossissent en diamètre, elles s’aplatissent en leur point d'arrêt (le centre de leur avant). Cet aplatissement s’amplifie avec l'augmentation du diamètre pour évoluer vers un creusement tendant à donner à la goutte d’eau de diamètre 6 mm une forme d’ombrelle, forme qui entraînera l’éclatement de la goutte en gouttes plus petites. Ceci explique qu’il n’existe pas de gouttes de pluie de diamètre supérieur à 6 mm.
说明
此文件中描述的项目
描绘内容
创作作者 简体中文(已转写)
某些值没有维基数据项目
知识共享署名-相同方式共享4.0国际 简体中文(已转写)
12 3 2016
媒体类型 简体中文(已转写)
image/png
数据大小 简体中文(已转写)
753,196 字节
2,216 像素
3,282 像素
文件历史
点击某个日期/时间查看对应时刻的文件。
| 日期/时间 | 缩略图 | 大小 | 用户 | 备注 | |
|---|---|---|---|---|---|
| 当前 | 2021年12月22日 (三) 09:53 |  | 3,282 × 2,216(736 KB) | Bernard de Go Mars | Erreur sur les diamètres 2 et 3 des gouttes qui sont 3 et 5 |
| 2016年3月13日 (日) 15:59 |  | 3,282 × 2,216(767 KB) | Bernard de Go Mars | Infos sur les rugosités étudiées par Achenbach. Remplacement du zéro impossible de l'échelle logarithmique. | |
| 2016年3月12日 (六) 17:25 |  | 3,263 × 2,196(709 KB) | Bernard de Go Mars | User created page with UploadWizard |
文件用途
没有页面使用本文件。
全域文件用途
以下其他wiki使用此文件:
- fr.wikipedia.org上的用途
- Nombre de Reynolds
- Discussion:Traînée
- Écoulement de Stokes
- Coefficient de traînée
- Discussion:Chute avec résistance de l'air
- Frottement fluide
- Forme d'une goutte de pluie
- Discussion:Frottement fluide
- Discussion:Forme d'une goutte de pluie
- Discussion utilisateur:Amaury67
- Trajectoire d'un projectile
- Crise de traînée
元数据
此文件中包含有扩展的信息。这些信息可能是由数码相机或扫描仪在创建或数字化过程中所添加。
如果此文件的源文件已经被修改,一些信息在修改后的文件中将不能完全反映出来。
| 水平分辨率 | 117.99 dpc |
|---|---|
| 垂直分辨率 | 117.99 dpc |