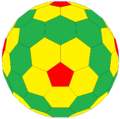
六角化五角化倒角十二面體
外观
 (单击查看旋转模型) | |||
| 類別 | 康威多面體 | ||
|---|---|---|---|
| 對偶多面體 | 截角五角化截半二十面體 | ||
| 數學表示法 | |||
| 康威表示法 | kt5daD | ||
| 性質 | |||
| 面 | 240 | ||
| 邊 | 360 | ||
| 頂點 | 122 | ||
| 歐拉特徵數 | F=240, E=360, V=122 (χ=2) | ||
| 對稱性 | |||
| 對稱群 | Ih群 | ||
| 圖像 | |||
| |||
在幾何學中,六角化五角化倒角十二面體是一種凸多面體,且屬於三角面多面體,乍看之下像是由正三角形組成,但實際上它是由多種不同的不等邊三角形所組成。
性質
[编辑]六角化五角化倒角十二面體可以由截角菱形三十面體在每個面加上錐體(Kleetope),接錐體的高為面到外接球的最長距離所組成的多面體,因此,六角化五角化倒角十二面體亦屬於康威多面體。
六角化五角化倒角十二面體共有240個面、360個邊、和122個頂點,由於其為凸多面體,且沒有破洞,因此歐拉示性數一樣是2。
歷史
[编辑]六角化五角化倒角十二面體為富勒提出的網格球頂之一,且於1954年6月申請專利獲准[1][2],而從獲准後專利生效的17年內建造的任何一種網格球頂或六角化五角化倒角十二面體形狀或結構的建築物都要支付富勒專利權稅[2],但實際上,該網格的設計與Bauersfeld的相同。[3]
此外,富勒提到,要構造這個多面體要從正二十面體開始,將每個面分個成若干個全等的正三角形,再將這些頂點投影在一個球面上,再將新的頂點構造成一個多面體就會變成這一個多面體,當然,三角形不再是等邊的。若再將頂點截去,就變成了截角六角化五角化倒角十二面體,此時,其結構就更接近球體,性質也更為接近球的特性了。[4]
1960年,富勒描述了若要建立一個巨型六角化五角化倒角十二面體體建築物的可行性,他提到:由16台大型塞考斯基直升機組成的飛行隊可在三個月內完成1.6公里高、3公里寬的半球,花費是兩億美元,並能涵蓋50個街區,防止雪落在屋子上,並控制日光的影響和空氣品質。[2]
圖像
[编辑]
一個六角化五角化倒角十二面體

一個六角化五角化倒角十二面體的展開圖
參建
[编辑]參考文獻
[编辑]- Deza, A.; Deza, M.; Grishukhin, V., Fullerenes and coordination polyhedra versus half-cube embeddings, Discrete Mathematics, 1998, 192 (1): 41–80 [2013-04-08], doi:10.1016/S0012-365X(98)00065-X, (原始内容存档于2007-02-06)
- Reprinted With Permission from Shelter, © 1973, Shelter Publications, Inc., Bolinas, Calif.
- VTML polyhedral generator(页面存档备份,存于互联网档案馆) Try "kt5daD" (康威多面體表示法)
- The Center for Spirituality & Sustainability. Siue.edu. [October 28, 2012]. (原始内容存档于2013-03-13).
- ^ Theoni Pappas. The magic of mathematics:discovering the spell of mathematica. 1994. ISBN 0933174993.
- ^ 2.0 2.1 2.2 Martin Pawley的Buckminster Fuller, Taplinger Publishing Co., New York, 1990
- ^ Bolinas, Calif. Geodesic Domes and Charts of the Heavens. Shelter Publications, Inc. [2013-04-14]. (原始内容存档于2020-11-12).
- ^ Theoni Pappas, 陳以鴻譯. 《數學放輕鬆》. 臺北縣新店市: 世茂出版社. 2004: P.257. ISBN 9577766110.
- Arratus Globe to the Zeiss Planetarium, Helmet, Werner, Publ. Gustav Fischer, Stuttgart, 1957.
- Letter to Shelter Publications from Dr. W. Degenhard, Carl Zeiss, June 19, 1973.
- James Clayton Lecture: Projection Planetarium and Shell Construction at Institution of Mechanical Engineering, London, May 10, 1957 by Professor Walter Bauersfeld.