原子堆積因子

在晶體學裡，原子堆積因子（或称APF）是計算一個晶體的體積裡原子體積佔的比例的函數。在計算前，必須假定原子是堅硬的球體，而且有確定的表面(而不是含糊不清的電子雲)。對只有一種元素的晶體來說，原子堆積因子的數學表示方法是：

\mathrm {APF} ={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\mathrm {crystal} }}}

在這裡，N_atoms 是一個晶體裡原子的數量，而V_atom 是每個原子的體積，而V_crystal是晶體的體積。目前發現最密的晶體的原子堆積因子值大約是0.74。

例子

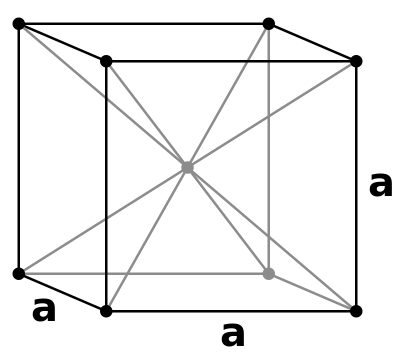
体心立方晶格的原胞在立方体的每一个角上含有八个原子，在中心含有一个原子。由于每一个角上的原子的体积都由相邻的晶胞共享，因此每一个体心立方晶胞含有两个原子。

每一个角上的原子都与中心的原子接触。从立方体的一个角到中心，然后再到另一个角的直线的长度为4r，其中r是原子的半径。根据几何，对角线的长度为a√3。因此，体心立方结构的每一条边的长度与原子的半径有以下的关系：

a={\frac {4r}{\sqrt {3}}}.

知道了球体的体积的公式后，便可以算出原子堆积因子：

\mathrm {APF} ={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\mathrm {crystal} }}}

={\frac {2(4/3)\pi r^{3}}{(4r/{\sqrt {3}})^{3}}}

={\frac {\pi {\sqrt {3}}}{8}}

\approx 0.68.\,\!

对于六方密堆积结构，也可进行类似的推导。把六边形的边长记为a，而把六边形的高记为c。那么：

a=2\times r

c=({\sqrt {\frac {2}{3}}})(4r).

于是便可以算出原子堆积因子：

\mathrm {APF} ={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\mathrm {crystal} }}}

={\frac {6(4/3)\pi r^{3}}{[(3{\sqrt {3}})/2](a^{2})(c)}}

={\frac {6(4/3)\pi r^{3}}{[(3{\sqrt {3}})/2](2r)^{2}({\sqrt {\frac {2}{3}}})(4r)}}

={\frac {6(4/3)\pi r^{3}}{[(3{\sqrt {3}})/2]({\sqrt {\frac {2}{3}}})(16r^{3})}}

={\frac {\pi }{\sqrt {18}}}

\approx 0.74.\,\!

利用类似的方法，所有晶体结构的原子堆积因子都可以求出。这里列出最常见的晶体结构的原子堆积因子，精确到小数点后第二位。

Schaffer, Saxena, Antolovich, Sanders, and Warner. The Science and Design of Engineering Materials Second Edition. New York: WCB/McGraw-Hill. 1999: 81–88.
Callister, W. Materials Science and Engineering Sixth Edition. San Francisco: John Wiley and Sons. 2002: 105–114.