示波器上的利萨茹图形
示波器上的利萨茹图形
 三维利萨茹图形
三维利萨茹图形
数学上,利萨茹(Lissajous)曲线(又称利萨茹图形、李萨如图形或鲍迪奇(Bowditch)曲线)是两个沿着互相垂直方向的正弦振动的合成的轨迹。
纳撒尼尔·鲍迪奇在1815年首先研究这一族曲线,朱尔·利萨茹在1857年作更详细研究。
利萨茹曲线由以下参数方程定义:

其中 ,
, 。
。
 称为曲线的参数,是两个正弦振动的频率比。若比例为有理数,则
称为曲线的参数,是两个正弦振动的频率比。若比例为有理数,则 ,参数方程可以写作:
,参数方程可以写作:
 ,
,
其中 。
。
- 若
 为无理数,曲线在长方形
为无理数,曲线在长方形![{\displaystyle [-a,a]\times [-b,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/148fdff4c46176677901bb62cb114820213de622) 中稠密。
中稠密。
- 若
 为有理数,
为有理数,
- 曲线是
 次代数曲线若
次代数曲线若![{\displaystyle \phi \in \left(0,{\frac {\pi }{2p}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506976e6d0a6d820ebbe4ebd3c761aba9326ff44) 对奇数
对奇数 ,或
,或 对偶数
对偶数 。
。
- 曲线是
 次代数曲线的一部分若
次代数曲线的一部分若 对奇数
对奇数 ,或
,或 对偶数
对偶数 。
。
- 若
 为偶数而
为偶数而 ,或若
,或若 为奇数而
为奇数而 ,则曲线是第
,则曲线是第 个切比雪夫多项式
个切比雪夫多项式 的曲线的一部分。
的曲线的一部分。
- 若
 ,
, ,则曲线是椭圆。
,则曲线是椭圆。
- 若
 ,则这椭圆其实是圆。
,则这椭圆其实是圆。
- 若
 ,则这椭圆其实是线段。
,则这椭圆其实是线段。
- 若
 ,
, (所以
(所以 ),则曲线是besace。
),则曲线是besace。
- 若
 ,则这besace是抛物线一部分。
,则这besace是抛物线一部分。
- 若
 ,则这besace是一个热罗诺双纽线。
,则这besace是一个热罗诺双纽线。
以下是利萨茹曲线的例子,其中 ,
, ,
,  是奇数,
是奇数, 是偶数,
是偶数, 。
。
-
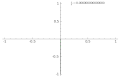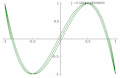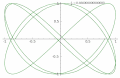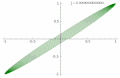
p = 1, q = 2
-
p = 3, q = 2
-
p = 3, q = 4
-
p = 5, q = 4
-
p = 5, q = 6
-
p = 9, q = 8
-
| Δφ
|
1:1
|
1:2
|
1:3
|
|
2:1
|
| 0
|

|

|

|
|

|
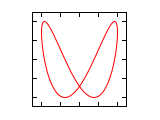
| ¹/₄·π
|

|
|

|
|

|
| ¹/₂·π
|

|

|

|
|

|
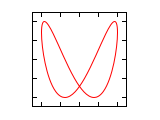
| ³/₄·π
|

|
|

|
|

|
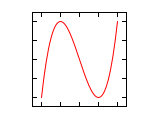
| 1·π
|

|

|
|
|

|
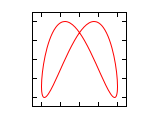
| 1¹/₄·π
|

|
|

|
|

|
| 1¹/₂·π
|

|

|

|
|

|
| 1³/₄·π
|

|

|

|
|

|
| 2·π
|

|

|

|
|

|
| Δφ
|
2:3
|
|
Δφ
|
3:4
|
| 0
|

|
|
0
|

|
| ¹/₂·¹/₄·π
|

|
|
¹/₃·¹/₄·π
|

|
| ¹/₂·¹/₂·π
|
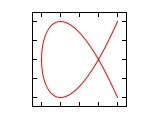
|
|
¹/₃·¹/₂·π
|

|
| ¹/₂·³/₄·π
|

|
|
¹/₃·³/₄·π
|

|
| ¹/₂·π
|

|
|
¹/₃·π
|

|
| 5/8·π
|

|
|
5/12·π
|

|
| ³/₄·π
|

|
|
¹/₂·π
|

|
| 7/8·π
|

|
|
7/12·π
|

|
| 1·π
|

|
|
²/₃·π
|

|
鼠标悬浮在两个数字上时,通过滚轮可以调节数字大小。
借由使用利萨茹图形可以测量出两个信号的频率比与相位差。






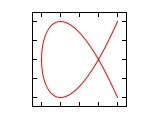





















![{\displaystyle [-a,a]\times [-b,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/148fdff4c46176677901bb62cb114820213de622)

![{\displaystyle \phi \in \left(0,{\frac {\pi }{2p}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506976e6d0a6d820ebbe4ebd3c761aba9326ff44)