辫群
 |
辫群（英语：Braid group）为数学领域中纽结理论的一个概念。一个 股的辫群（记为）是元素为 n-braid 的群，其运算为前一个 n-braid 按后一个 n-braid 的方式操作（见 § 举例说明）。
而辫群是由埃米尔·阿廷(1925[1])提出的，因此又被称为阿廷辫群（英语：Artin Braid group）。[2]
引言
[编辑]想像有4条横著摆放的绳子，它们的两端分别被固定在左右两侧的墙上，如下图所示，黑点代表被固定的位置。
我们称这样绳子的摆放方式，或是编织的方式为一个辫子（英语：braid）。而正式的写法中会连绳子的数目也一起表达，将4股的辫子以英文简写成 4-braid。
如果将刚才的辫子中下面两条的右端交换位置，会变成下图的样子。
那么这两种会是不同的4股辫子( 英语：4-braid)。 如果将这两种辫子理解为群中的元素，那么刚才把右端交换位置的操作就是群当中的运算。在辫群的讨论中，常用这些操作来表示不同的辫子，这种表示方法称作 braid word。[2]
举例说明
[编辑]在这个小节中，以为例。
下面的两条辫子是不同的：
|
|
不同于 | 
|
但是下面的两条辫子是相同的：
|
|
同于 | 
|
所有的股都必须从左向右移动，所以下面的图片并不是一条辫子：
|
不是辫子 |
我们可以编两条辫子：
|
加 | 
|
等于 | 
|
另一个例子：
|
|
加 |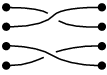 
|
等于 | 
|
复合 / 编织物σ和τ的组成写为στ。
是四股上所有编织物的集合。上面的复合是群操作，单位元是四股水平平行股的辫子，辫子B的逆元素是取消B的操作。
应用
[编辑]辫群的应用包括 陈-西蒙斯理论、亚历山大定理（Alexander's Theorem）、杨-巴克斯特方程、 代数几何、任意子、等。[3]
参见
[编辑]参考文献
[编辑]- ^ 陈国璋(Kuo-Chang Chen). 利用辮群設計支援可比較搜尋之加密法: 46. 2010 [2023-03-25].
- ^ 2.0 2.1 Weisstein, Eric W. Braid Group. MathWorld--A Wolfram Web. [2023-03-25]. （原始内容存档于2023-03-25）.
- ^ Cohen, Daniel; Suciu, Alexander. The Braid Monodromy of Plane Algebraic Curves and Hyperplane Arrangements. Commentarii Mathematici Helvetici. 1997, 72 (2): 285–315. arXiv:alg-geom/9608001
. doi:10.1007/s000140050017.
- ^ Boyland, Philip L.; Aref, Hassan; Stremler, Mark A., Topological fluid mechanics of stirring (PDF), Journal of Fluid Mechanics, 2000, 403 (1): 277–304, Bibcode:2000JFM...403..277B, MR 1742169, doi:10.1017/S0022112099007107, （原始内容 (PDF)存档于2011-07-26）
- ^ Gouillart, Emmanuelle; Thiffeault, Jean-Luc; Finn, Matthew D., Topological mixing with ghost rods, Physical Review E, 2006, 73 (3): 036311, Bibcode:2006PhRvE..73c6311G, MR 2231368, arXiv:nlin/0510075 , doi:10.1103/PhysRevE.73.036311
- ^ Stremler, Mark A.; Ross, Shane D.; Grover, Piyush; Kumar, Pankaj, Topological chaos and periodic braiding of almost-cyclic sets (PDF), Physical Review Letters, 2011, 106 (11): 114101, Bibcode:2011PhRvL.106k4101S, doi:10.1103/PhysRevLett.106.114101
