奈克方块
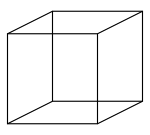
奈克方块(Necker cube),或称为内克尔立方体,是一个错视的图像,由瑞士晶体学家路易斯·艾伯特·奈克在其1832年发表的论文中首次提出[1]。
奈克方块是一个由12条线组成的图像,是等大透视的角度绘画一个立方体,等长的平行线不论其远近,在图中会画成等长的平行线,其中没有任何关于立体的资讯。因此对于立方体的放置位置及观看角度会有模棱两可的诠释。
有歧义性的图
[编辑]

奈克方块是个有歧义性的图,一种诠释方式是在一个较高位置看透明立方体的俯视图,另一种诠释方式是在一个较低位置看透明立方体的仰视图。
人类的视觉系统在接收这类的图像时,会设法诠释图像的各部份,使整体的图像没有矛盾之处。有时会用奈克方块来测试人人类视觉系统的电脑模型,测试电脑模型是否可以像人类视觉系统一样的诠释这个图象。
大多数的人在看奈克方块时,会将左前方的面视为立方体最接近观察者的一面,也许是因为人们在物体上方俯视物体的机率远高于物体下方仰视物体的情形,因此大脑倾向以这个的方式来诠释图像。

人类在观看奈克方块时,不会对方块的各部份有不一致的诠释。若有不一致的诠释,其结果可能会类似不可能立方体,是不可能物体的一种。
由奈克方块可以看出人类视觉系统的一些特性。人类诠释奈克方块的方式可以说明人脑有类似类神经网路的特性,存在二个不一样,但都可以互换的稳定状态[2]。西德尼·布拉德福在出生后10个月就失明,在52岁时接受手术恢复视力,他观看奈克方块时不会像一般人有模棱两可诠释的情形。[3]。
知识论
[编辑]在知识论中用奈克方块的例子来反对素朴实在论,素朴实在论认为我们以世界实际存在的样子来认知这个世界。但在奈克方块的例子中,我们可以看到二种不同的立方体(或二种中的一种),但事实上没有立方体,只有一个由12条线组成的二维图形,我们看到的是没有实际存在的物体,因此否定了素朴实在论。这个例子可以用来支持表现实在论。
旋转的奈克方块可用来说明人类的视觉系统会有一种称为“cue recruitment”的现象,会影响我们对图象的认知方式。
相关条目
[编辑]参考资料
[编辑]- ^ Necker, L. A. Observations on some remarkable optical phaenomena seen in Switzerland; and on an optical phaenomenon which occurs on viewing a figure of a crystal or geometrical solid. London and Edinburgh Philosophical Magazine and Journal of Science. 1832, 1 (5): 329–337.
- ^ Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. W. H. Freeman. Reprint: The MIT Press. 1982. ISBN 0-7167-1284-9.
- ^ Gregory, R. The Blind Leading the Sighted: An Eye-Opening Experience of the Wonders of Perception (pdf). Nature. August 2004, 430 (7002) [2012-08-22]. PMID 15318199. doi:10.1038/430836a. (原始内容存档 (PDF)于2012-11-19).
