定义域著色

函数 f(x) = (x² − 1)(x − 2 − i)²/x² + 2 + 2i的定义域著色函数图形。 色调表示其函数值的辐角，而饱和度和明度表示其函数值的绝对值，这种上色方式又称为色相环法

函数 f(x) = (x² − 1)(x − 2 − i)²/x² + 2 + 2i的另一种定义域著色函数图形。 以上色网格和等值线的方式来呈现。

在复分析中，定义域著色是一种可以将复变函数可视化的一个资讯视觉化技术，是借由在定义域上以色彩表示其函数值来表达函数图形的方法，故称为“定义域”著色。“定义域著色”一词由法兰克·菲莉丝（英语：Frank Farris）在1998年左右时命名。其上色方法有很多种，最常见的是色相环复变函数图形，以其辐角值对应色相的颜色来上色，亦有使用其他色彩空间作为上色依据的定义域著色的复变函数图形。早期有许多做法是将其辐角或相位利用对应色相的颜色以等值线的方式来呈现资料。 1999年，乔治·艾柏德和保罗·戈弗雷则使用了连续的颜色将点从定义域映射到值域或像平面，而在1997年以前，道格拉斯·阿诺德是使用著色的网格来呈现复变函数。威葛特·伊里亚斯也在其教科书详细的介绍了一种定义域著色的一种变体——相位图。

动机

维度不够

实数值函数 f : ℝ → ℝ (例如 f(x) = x²) 可以被 绘制在二维平面的直角坐标系上。

复数值函数 g : ℂ → ℂ 虽然只有一个变数，但是因为是复数，因此需要使用复数高斯平面才能呈现。高斯平面是一个二维的空间，而要表示的定义域和值域也都是复数域，因此各需要2个维度，因此要完全呈现复变函数图形需要使用四维空间才能呈现，这使得复变函数难以在三维空间中可视化。有一种描述全纯函数的方式是使用黎曼曲面。

复数可视化的模式

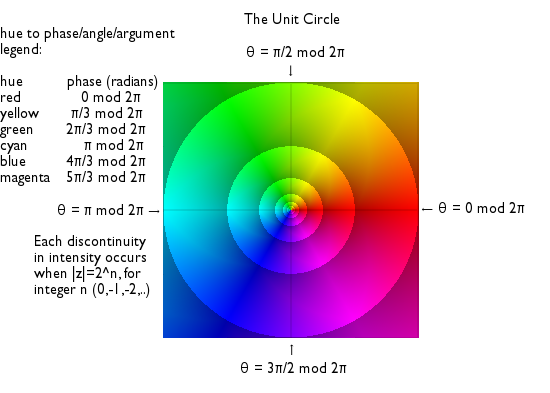
给定一个复数$z$，其可以被表示为$z=a+bi$形式，也可以表示成$z=re^{i\theta }$，其辐角$\theta$是一个角度值，可以使用有周期性的资料表示，例如颜色的色调，其模$r=\left|z\right|$可由强度或强度变化表示。色调的排列是任意的，但通常会以色相环的色调为主，例如色相环复变函数图形。有时复数的辐角会由特定的梯度表示，而不使用色调表示。

绘制方法

定义域著色有很多种呈现方式，例如以等值线或网格上色，也有使用连续颜色上色。

下图显示了正弦函数w = sin z，实轴从−2π到2π、虚轴从−1.5到1.5。

参见

• 色相环复变函数图形：一种使用HSV基于色相和饱和度作为上色依据的定义域著色方法