应力-应变曲线

某一种特定材料的应力与应变关系称为该材料的应力-应变曲线（stress-strain curve）。每一种材料都有唯一的应力-应变曲线，该曲线可以通过记录材料在不同的拉伸和压缩加载（应力）下的形变（应变）来获得。这条曲线也提供了很多该材料的特性，例如其弹性模量、降伏强度（弹力限）、极限拉伸强度，也可以看出材料是脆性材料还是延展性材料^[1]。

一般而言，有关任何变形下，应力和应变的关系都可以视为是应力-应变曲线。应力和应变可以是正应力及正应变，剪应力及剪应变，也可以是混合的。可以是单一轴向、双轴或是多轴的，甚至可以是时变的。变形可以是压缩、拉伸、扭转、转动等。若没有特别标明，应力-应变曲线是指在拉伸测试下正向应力及正向应变之间的关系。

考虑一截面积为A的棒状物体，其两端施加大小相等，方向相反的拉伸力。材料会受到应力（定义为受力和其截面积之间比值），也会有轴向的伸长：

\mathrm {\sigma } ={\tfrac {F}{A_{0}}}

\mathrm {\epsilon } ={\tfrac {L-L_{0}}{L_{0}}}={\tfrac {\Delta L}{L_{0}}}

其中下标0是材料的原始尺寸，应力的SI单位是牛顿每平方米（N/m²），或是Pa（1 Pa = 1 N/m²），应变为无因次量。

在拉伸试验下，记录不同应变下，材料应力的变化，一直到材料断裂为止，描绘其曲线，即为应力-应变曲线。一般而言，应力-应变曲线会用应变为x轴，应力为y轴。为了工程的需求，一般会假设材料在整个拉伸过程中，其截面积不会变化，不过在变形过程中，截面积也会略为变小。在假设截面积不变的条件下所画的应力-应变曲线称为“工程应力-应变曲线”，考虑真正截面积变化的应力-应变曲线称为“真应力-应变曲线”。

曲线的不同阶段

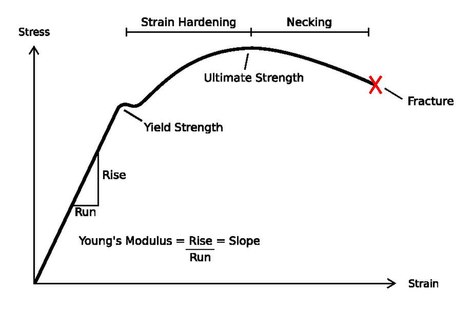
右图是室温下低碳钢的应力-应变曲线，曲线的不同阶段有不同的特性，也有不同的机械性质。而其他材料也可能会省略其中的一些阶段，或是出现其他的阶段。

第一阶段是线性弹性阶段。此阶段的应力和应变成正比，遵守胡克定律，其斜率即为杨氏模量。材料在这个阶段的变形都是弹性变形，此阶段的结束是塑性变形的开始，该点的应力即为降伏强度（或是上降伏点，简称UYP）。

第二阶段是应变硬化阶段。其应力超过降伏强度，小于极限强度（ultimate strength point）。极限强度是应力-应变曲线的最高点。这个区域一开始的应力不随应变变化，有短暂的水平区，之后，其应力随著材料伸长而变大。平坦区的应力称为下降伏点（LYP），是因为赖得带（英语：Lüders band）的形成及传递所造成。明显的，非均质塑性变形会在上降伏强度形成赖得带，将变形扩散到下降伏强度的材料。当材料再度均匀变形时，随著材料的伸展，其应力会增加，这称为加工硬化。因为塑性变形引起的致密位错使位错无法再进一步发展。为了要克服这种阻碍，需要加较大的临界分解剪应力（英语：resolved shear stress）。在应变累积时，材料也就在进行加工硬化，一直到应力到达极限强度为止。

第三阶段是颈缩阶段，应力超过极限强度后，试料中会出现颈缩（Necking）现象，也就是某一段的截面积明显比平均截面积要小。颈缩变形是非均质的，因为应力在截面积较小的区域更容易集中，因此颈缩会自我增强，让应力更集中。这种正回授会让颈缩很快就生成，并且很快断裂。不过此时拉力虽在减少，但其加工硬化仍在进行中。此时用真实截面积计算的真应力会继续增加，但假设截面积不变的工程应力就会减少。第三阶段的最后是材料的断裂。在断裂后可以计算材料的伸长量以及截面积的缩减量。

真实应力和应变之间的关系

真实应力和应变的关系会考虑到截面积缩小对应力的影响，以及因应变参考长度使用当时长度（而不是原始长度）造成的应变降低，和工程应力及应变之间的关系有些不同。

\mathrm {\sigma _{t}} ={\tfrac {F}{A}}

\mathrm {\epsilon _{t}} =\int {\tfrac {\delta L}{L}}

此处的尺寸是即时值，假设物体体积守恒，变形是均匀的出现。 $A_{0}L_{0}=AL$

真实应力和应变可以用工程应力及应变表示。针对真实应力

$\mathrm {\sigma _{t}} ={\tfrac {F}{A}}={\tfrac {F}{A_{0}}}*{\tfrac {A_{0}}{A}}={\tfrac {F}{A_{0}}}*{\tfrac {L}{L_{0}}}=\sigma (1+\epsilon )$

针对应变

$\mathrm {\delta \epsilon _{t}} ={\tfrac {\delta L}{L}}$

两边积分，再考虑边界条件

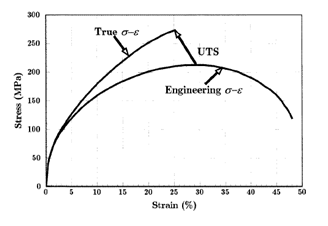
$\mathrm {\epsilon _{t}} =ln({\tfrac {L}{L_{0}}})=ln(1+\epsilon )$

因此在张力测试中，真实应力会大于工程应力，真实应变小于工程应变。在真实应力-应变图上有一个点，而其对应的等效工程应力及应变点会往左上方移。真实应力及工程应力的差值会随著塑性变形增加而变大。在低应变时（例如线性形变），两者的差值可以省略。对于抗张强度的点，是工程应力-应变曲线的最大点，但不是真应力-应变曲线的最大点。因为工程应力和施力成正比，颈缩形变的判断基准可以用 $\mathrm {\delta {\textit {F}}} =0$ 来计算：

$\mathrm {\delta {\textit {F}}} =0=\sigma _{t}\delta A+A\delta \sigma _{t}$

$\mathrm {-{\tfrac {\delta A}{A}}} =\mathrm {\tfrac {\delta \sigma _{t}}{\sigma _{t}}}$

上述分析考虑到抗张强度的本质，抗张强度点时，加工硬化（又称应变硬化）的效果恰好和截面积减少的效果相抵消。

在颈缩形变后，材料承受的是非均质的形变，因此上述公式不再有效。颈缩时的应力及应变可以表示为：

\mathrm {\sigma _{t}} ={\tfrac {F}{A_{neck}}}

\mathrm {\epsilon _{t}} =ln({\tfrac {A_{0}}{A_{neck}}})

以下的经验式常用来描述真实应力和应变之间的关系。

$\mathrm {\sigma _{t}} =K(\epsilon _{t})^{n}$

上述的n是应变硬化系数，K是强度系数。n可以用来衡量材料加工硬化的特化，n越大的越不容易颈缩。一般而言，金属在室温下的n从0.02至0.5之间^[2]

分类

在许多不同的材料中，可以依应力-应变曲线的特性将材料分为二类：分别是延展性（ductile）材料及脆性（brittle）材料^[3]。

延展性材料

具有延展性的材料，包括结构钢，以及许多其他金属的合金，可以依其在室温下降伏的情形来区分其特性^[4]。

低碳钢的应力-应变关系，在降伏强度以下都非常的线性，这段线性区域即为弹性区，斜率为弹性模量或杨氏模量。许多延展性的材料（包括一些金属、塑料以及陶瓷）都有降伏点。塑性流动从上降伏点开始，在下降伏点继续塑性流动。在下降伏点时，永久变形会在试料中不均匀的分布。在上降伏点形成的变形带会在下降伏点时延著标距长度传播。在鲁德（luders）应变时，变形带会占据整个标距长度。超过这点后，就会出现加工硬化。降伏点的出现对应材料中差排的钉扎点。例如在差排处出现固溶体，就会有钉扎点的效果，使差排无法再移动。因此，需要较大的力才能使差排再移动。若差排离开钉扎点，需要的应力就会比较小。

应变超过降伏点后，因为差排离开科氏气团（英语：Cottrell atmosphere），曲线会略为下降。若继续变形，会因为应变硬化（英语：Strain hardening）而使应力增加，直到到达极限拉伸强度为止。到达时，会因为泊松收缩的影响使截面积减少。因此试料开始颈缩，最后会断裂。

延展性材料的颈缩和系统的几何不稳定性有关。因为材料本身天然的不均匀，常会出现有些区域有夹杂小杂质或是出现小孔，可能是在表面或是内部，其应变会集中，让这些区域面积比其他区域要小。在应变小于极限拉伸应变时，区域加工硬化的的应力增加率比面积缩减率要大，因此这些区域比其他区域更不容易变形，此情形下就没有几何不稳定性，也就是说，在极限拉伸应变之前，材料可以让不均匀的影响降低。不过若应变继续增加，加工硬化的效果会下降，截面较小的区域就会比其他区域要脆弱，面积减小会集中在这些区域，颈缩会越来越明显，直到材料断裂为止。当材料出现颈缩的情形，塑性变形会集中在颈缩部位，材料其他部份仍维持弹性变形。

延展性材料的应力-应变曲线可以用Ramberg-Osgood方程来近似^[5]，此方程应用上很直接，只需要材料极限拉伸强度、降伏强度、杨氏模量及伸长比例即可。

脆性材料

脆性材料（例如铸铁、玻璃及石头等）在受到拉伸时，会在长度还没有明显变化时就先断裂了^[6]，有些则是在降服点之前才断裂。

像混凝土或是碳纤维之类的脆性材料没有明确定义的降服点，也没有应变硬化的现象，因此其最大强度等于断裂强度。像玻璃也是脆性材料，没有塑性变形，在弹性变形的过程中就断裂了。这类脆性材料在拉伸变形过程没有颈缩现象，将断裂的二部份重新组合，形状会和原来完全一样。脆性材料的典型应力-应变曲线是线性的。有些材料（如混凝土）的抗拉强度远低于拉压强度，因此在工程应用中，会假设其抗拉强度为零。玻璃纤维的抗拉强度比钢要大，而一整块的玻璃无此特性，这是因为和材料中缺陷有关的应力强度因子所造成的。当试样尺寸越大，缺陷的大小也随之加大。一般而言，绳子的抗拉强度会小于个别纤维抗拉强度的总和。

影响因子

不同材料的应力-应变曲线会有很大的变化，是不同内在结构及组成的结果。因为外在因素的不同，相同种类的材料进行多次的拉伸实验，也会有不同的结果，主要会依试件的温度以及加载的速度而不同。不过若在进一步的描，内在因素和外在因素的分界不是非常的明确。许多因素会影响应力-应变曲线，例如改变杨氏模数、硬化程度，也有可能改变结构以及其组成。

在应力-应变曲线中，常会忽略时间的影响，不过若应变率较高，其应力也会较大，其关系如下

$\mathrm {\sigma _{t}} =K({\dot {\epsilon }}_{T})^{m}$

其中的m是应变率敏感度。m越大时，材料抵抗颈缩的能力也越大。就像加工硬化系数的效果一样

另一个主要影响因素是温度。温度会影响差排及扩散的活化程度。脆性材料可能会因为温度上升而变成延展性材料。

参考来源

^ Luebkeman, C., & Peting, D. (2012, 04 28).
^ Courtney, Thomas. Mechanical behavior of materials. Waveland Press, Inc. 2005: 6–13.
^ Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 51.
^ Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 58.
^ Mechanical Properties of Materials. （原始内容存档于2019-05-04）.
^ Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 59.

外部链接

British Society for Strain Measurement （页面存档备份，存于互联网档案馆）
Stress–strain diagram
Engineering stress–strain curve （页面存档备份，存于互联网档案馆）

[1] Luebkeman, C., & Peting, D. (2012, 04 28).

[2] Courtney, Thomas. Mechanical behavior of materials. Waveland Press, Inc. 2005: 6–13.

[3] Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 51.

[4] Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 58.

[5] Mechanical Properties of Materials. （原始内容存档于2019-05-04）.

[6] Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 59.

[1]

[2]

[3]

[4]

[5]

[6]