波函数

本条目中，向量与标量分别用粗体与斜体显示。例如，位置向量通常用 $\mathbf {r} \,\!$ 表示；而其大小则用 $r\,\!$ 来表示。

提示：此条目的主题不是波动方程式。

设想经典力学里的谐振子 系统（A-B），一条弹簧的一端固定不动，另一端有一个带质量圆球；在量子力学里， （C-H）展示出同样系统的薛丁格方程式的六个波函数解。横轴坐标表示位置，竖轴坐标表示波函数机率幅的实部（蓝色）或虚部（红色）。（C-F）是定态，（G、H）不是定态。定态的能量为驻波振动频率与约化普朗克常数的乘积。

在量子力学里，量子系统的量子态可以用波函数（英语：Wave function）来描述。薛丁格方程式设定波函数如何随著时间流逝而演化。

波函数 $\Psi (\mathbf {r} ,t)$ 是一种复值函数，表示粒子在位置 $\mathbf {r}$ 、时间 $t$ 的机率幅，它的绝对值平方 $|\Psi (\mathbf {r} ,t)|^{2}$ 是在位置 $\mathbf {r}$ 、时间 $t$ 找到粒子的机率密度。以另一种角度诠释，波函数$\Psi (\mathbf {r} ,t)$是“在某时间、某位置发生相互作用的概率幅”。

历史

路易·德布罗意

埃尔温·薛丁格

在1920年代与1930年代，理论量子物理学者大致分为两个阵营。第一个阵营的成员主要为路易·德布罗意和埃尔温·薛丁格等等，他们使用的数学工具是微积分，他们共同创建了波动力学。第二个阵营的成员主要为维尔纳·海森堡和马克斯·玻恩等等，使用线性代数，他们建立了矩阵力学。后来，薛丁格证明这两种方法完全等价。

德布罗意于1924年提出的德布罗意假说表明，每一种微观粒子都具有波粒二象性。电子也不例外，具有这种性质。电子是一种波动，是电子波。电子的能量与动量分别决定了它的物质波频率与波数。既然粒子具有波粒二象性，应该会有一种能够正确描述这种量子特性的波动方程式，这点子给予埃尔温·薛定谔极大的启示，他因此开始寻找这波动方程式。薛定谔参考威廉·哈密顿先前关于牛顿力学与光学之间的类比这方面的研究，在其中隐藏了一个奥妙的发现，即在零波长极限，物理光学趋向于几何光学；也就是说，光波的轨道趋向于明确的路径，而这路径遵守最小作用量原理。哈密顿认为，在零波长极限，波传播趋向于明确的运动，但他并没有给出一个具体方程式来描述这波动行为，而薛定谔给出了这方程式。他从哈密顿-雅可比方程成功地推导出薛定谔方程式。他又用自己设计的方程式来计算氢原子的谱线，得到的答案与用波耳模型计算出的答案相同。他将这波动方程式与氢原子光谱分析结果，写为一篇论文，1926年，正式发表于物理学界。从此，量子力学有了一个崭新的理论平台。

薛丁格给出的薛定谔方程式能够正确地描述波函数的量子行为。那时，物理学者尚未能解释波函数的涵义，薛定谔尝试用波函数来代表电荷的密度，但遭到失败。1926年，玻恩提出机率幅的概念，成功地解释了波函数的物理意义。可是，薛定谔本人不赞同这种统计或机率方法，和它所伴随的非连续性波函数塌缩，如同爱因斯坦认为量子力学只是个决定性理论的统计近似，薛定谔永远无法接受哥本哈根诠释。在他有生最后一年，他写给玻恩的一封信内，薛定谔清楚地表明了这意见。

1927年，道格拉斯·哈特里与弗拉基米尔·福克在对于多体波函数的研究踏出了第一步，他们发展出哈特里－福克方程来近似方程的解。这计算方法最先由哈特里提出，后来福克将之加以改善，能够符合包立不相容原理的要求。

薛定谔方程式不具有劳仑兹不变性 ，无法准确给出符合相对论的结果。薛定谔试著用相对论的能量动量关系式，来寻找一个相对论性方程式，并且描述电子的相对论性量子行为。但是这方程式给出的精细结构不符合阿诺·索末菲的结果，又会给出违背量子力学的负机率和怪异的负能量现象，他只好将这相对论性部分暂时搁置一旁，先行发表前面提到的非相对论性部分。

1926年，奥斯卡·克莱因和沃尔特·戈尔登将电磁相对作用纳入考量，独立地给出薛定谔先前推导出的相对论性部分，并且证明其具有劳仑兹不变性。这方程式后来称为克莱因-戈尔登方程式。

1928年，保罗·狄拉克最先成功地统一了狭义相对论与量子力学，他推导出狄拉克方程式，适用于电子等等自旋为1/2的粒子。这方程式的波函数是一个旋量，拥有自旋性质。

概述

在一维无限深方形阱内，粒子的能级与对应的波函数。

在一维无限深方形阱内，找到能级为 $n$ 的粒子的机率。

位置空间波函数

假设一个自旋为零的粒子移动于一维空间。这粒子的量子态以波函数表示为 $\Psi (x,t)$ ；其中，$x$ 是位置，$t$ 是时间。波函数是复值函数。测量粒子位置所得到的结果不是决定性的，而是机率性的。粒子的位置 $x$ 在区间 $[a,b]$ （即 $a\leq x\leq b$ ）的机率$P_{a\leq x\leq b}$为

$P_{a\leq x\leq b}=\int _{a}^{b}\,|\Psi (x,t)|^{2}\mathrm {d} x$ ；

其中，$t$ 是对于粒子位置做测量的时间。

换句话说，$|\Psi (x,t)|^{2}$ 是粒子在位置 $x$ 、时间 $t$ 的机率密度。

这导致归一化条件：在位置空间的任意位置找到粒子的机率为100%：

$\int _{-\infty }^{\infty }\,|\Psi (x,t)|^{2}\mathrm {d} x=1$ 。

动量空间波函数

在动量空间，粒子的波函数表示为 $\Phi (p,t)$ ；其中，$p$ 是一维动量，值域从 $-\infty$ 至 $+\infty$ 。测量粒子动量所得到的结果不是决定性的，而是机率性的。粒子的动量 $p$ 在区间 $[a,b]$ （即 $a\leq p\leq b$ ）的机率为

$P_{a\leq p\leq b}=\int _{a}^{b}\,|\Phi (p,t)|^{2}\mathrm {d} p$ 。

动量空间波函数的归一化条件也类似：

$\int _{-\infty }^{\infty }\,\left|\Phi (p,t)\right|^{2}\mathrm {d} p=1$ 。

两种波函数之间的关系

本图展示一维零自旋自由粒子的波函数范例，左边是位置空间波函数 $\Psi (x)$ 的实部（紫色）和机率密度 $|\Psi (x)|^{2}$ （红色），右边是动量空间波函数 $\Phi (p)$ 的实部（金色）和机率密度 $|\Phi (p)|^{2}$ （蓝色）。在x-轴的某位置 $x$ 或p_x-轴的某动量 $p$ 显示出的粒子颜色的不透明度，分别表示在那位置 $x$ 或动量 $p$ 找到粒子的机率密度（不是波函数的机率幅）。

位置空间波函数与动量空间波函数彼此是对方的傅立叶变换。他们各自拥有的信息相同，任何一种波函数都可以用来计算粒子的相关性质。两种波函数之间的关系为

$\Phi (p,t)={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\infty }^{\infty }\,e^{-ipx/\hbar }\Psi (x,t)\mathrm {d} x$ 、

$\Psi (x,t)={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\infty }^{\infty }\,e^{ipx/\hbar }\Phi (p,t)\mathrm {d} p$ 。

波函数实质

量子力学中体系的态实际上由一个希尔伯特空间里的 $|{\mathfrak {J}}(t)\rangle$ 矢量来描述。我们可以用任何不同的基来表示它。

波函数 $\Psi (x,t)$ 实际上是 $|{\mathfrak {J}}(t)\rangle$ 在坐标本征函数为基上展开的$x$“分量”：

$\Psi (x,t)=\langle x\mid {\mathfrak {J}}(t)\rangle ,$

（这里基矢量 $|x\rangle$ 对应于本征值为 $x$ 的算符 ${\hat {x}}$ 的本征函数）。

动量空间波函数 $\Phi =(p,t)$ 是 $|{\mathfrak {J}}(t)\rangle$ 用动量本征函数的基展开时的展开系数:

$\Phi (p,t)=\langle p\mid {\mathfrak {\Im }}(t)\rangle$

（这里基矢量 $|p\rangle$ 对应于属于本征值 $p$ 的 ${\hat {p}}$ 的本征函数） 。

我们也可以把 $|{\mathfrak {F}}(t)\rangle$ 用能量本征函数的基展开（简单起见，假设谱是分立的）：

$c_{n}(t)=\langle n\mid {\mathfrak {\Im }}(t)\rangle$

（这里基矢量 $|n\rangle$ 对应属于 ${\hat {H}}$ 的第 $n$ 个本征函数：$c_{n}=\left\langle f_{n}\mid \Psi \right\rangle =\int f_{n}(x)^{*}\Psi (x,t)\mathrm {d} x$) 。

波函数 $\Psi$ 与 $\Phi$ 和系数的集合 $\left\{c_{n}\right\}$ ，所有这些所表示的都是同一个状态，包含完全一样的信息——它们仅是描述同一矢量的三种不同途径而已：

$|{\mathfrak {J}}(t)\rangle \rightarrow \int \Psi (y,t)\delta (x-y)dy=\int \Phi (p,t){\frac {1}{\sqrt {2\pi \hbar }}}e^{ipx/\hbar }dp=\sum c_{n}e^{-iE_{n}t/\hbar }\psi _{n}(x)$

薛丁格方程式

在一维空间里，运动于位势 $V(x)$ 的单独粒子，其波函数满足含时薛丁格方程式

$-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial x^{2}}}\Psi (x,t)+V(x)\Psi (x,t)=i\hbar {\frac {\partial }{\partial t}}\Psi (x,t)$ ；

其中，$m$ 是质量，$\hbar$ 是约化普朗克常数。

不含时薛丁格方程式与时间无关，可以用来计算粒子的本征能量与其它相关的量子性质。应用分离变数法，猜想 $\Psi (x,\,t)$ 的函数形式为

$\Psi (x,\,t)=\psi _{E}(x)e^{-iEt/\hbar }$ ；

其中，$E$ 是分离常数，稍加推导可以论定 $E$ 就是能量，$\psi _{E}(x)$ 是对应于 $E$ 的本征函数。

代入这猜想解，经过一番运算，可以推导出一维不含时薛丁格方程式：

$-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial x^{2}}}\psi _{E}(x)+V(x)\psi _{E}(x)=E\psi _{E}(x)$ 。

波函数的概率诠释

波函数 $\Psi (\mathbf {r} ,t)$ 是概率波。其模的平方 $\vert \Psi (\mathbf {r} ,t)\vert ^{2}\,$ 代表粒子在该处出现的概率密度，并且具有归一性，全空间的积分

$\int \vert \Psi (\mathbf {r} ,t)\vert ^{2}\,d^{3}\,x=1$ 。

波函数的另一个重要特性是相干性。两个波函数叠加，概率的大小取决于两个波函数的相位差，类似光学中的杨氏双缝实验。

波函数的本征值和本征态

在量子力学中，可观察量 $A$ 以算符 ${\hat {A}}$ 的形式出现。${\hat {A}}$ 代表对于波函数的一种运算。例如，在位置空间里，动量算符 ${\hat {\mathbf {p} }}$ 的形式为

${\hat {\mathbf {p} }}=-i\hbar \nabla$ 。

可观察量 $A$ 的本征方程式为

${\hat {A}}\psi =a\psi$ 。

对应的 $a$ 称为算符 ${\hat {A}}$ 的本征值，$\psi$ 称为算符 ${\hat {A}}$ 的本征态。假设对于 ${\hat {A}}$ 的本征态 $\psi$ 再测量可观察量 $A$ ，则得到的结果是本征值 $a$ 。

态叠加原理

假设对于某量子系统测量可观察量 $A$ ，而可观察量 $A$ 的本征态 $|a_{1}\rangle$ 、$|a_{2}\rangle$ 分别拥有本征值 $a_{1}$ 、$a_{2}$ ，则根据薛定谔方程的线性关系，叠加态 $|\psi \rangle$ 也可以是这量子系统的量子态：

$|\psi \rangle =c_{1}|a_{1}\rangle +c_{2}|a_{2}\rangle$ ；

其中， $c_{1}$ 、$c_{2}$ 分别为叠加态处于本征态 $|a_{1}\rangle$ 、$|a_{2}\rangle$ 的机率幅。

假设对这叠加态系统测量可观察量 $A$ ，则测量获得数值是 $a_{1}$ 或 $a_{2}$ 的机率分别为 $|c_{1}|^{2}$ 、$|c_{2}|^{2}$ ，期望值为

$\langle \psi |A|\psi \rangle =|c_{1}|^{2}a_{1}+|c_{2}|^{2}a_{2}$ 。

定态

描述谐振子的含时薛丁格方程式的三个波函数解。左边：波函数机率幅的实部（蓝色）或虚部（红色）。右边：找到粒子在某位置的机率，这说明了为甚么机率与时间无关的量子态被称为“定态”。上面两个横排是定态，最下面横排是叠加态 $\psi _{N}=(\psi _{0}+\psi _{1})/{\sqrt {2}}$ 。

在量子力学中，一类基本的问题是哈密顿算符 ${\hat {H}}$ 不含时间的情况。对于这问题，应用分离变数法，可以将波函数 $\Psi (\mathbf {r} ,t)$ 分离成一个只与位置有关的函数 $\psi (\mathbf {r} )$ 和一个只与时间有关的函数 $f(t)$ ：

$\Psi (\mathbf {r} ,t)=\psi (\mathbf {r} )f(t)$ 。

将这公式代入薛定谔方程，就会得到

$f(t)=\exp {(-iEt/\hbar )}$ 。

而 $\psi (\mathbf {r} )$ 则满足本征能量薛丁格方程式：

${\hat {H}}\psi (\mathbf {r} )=E\psi (\mathbf {r} )$ 。

例子

自由粒子

主条目：自由粒子

3D空间中的自由粒子，其波矢 为k ， 角频率 为ω，其波函数为：

$\Psi (\mathbf {r} ,t)=Ae^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}\,.$

无限深方形阱

主条目：无限深方形阱

粒子被限制在x = 0和x = L之间的1D空间中，其波函数为:

${\begin{aligned}\Psi (x,t)&={\sqrt {\frac {2}{L}}}\sin \left({\frac {n\pi x}{L}}\right)e^{-i\omega _{n}t},&\quad 0\leq x\leq L\\\Psi (x,t)&=0,&x<0,x>L\\\end{aligned}}$

其中，$\hbar \omega _{n}={\frac {n^{2}h^{2}}{8mL^{2}}}$是能量本征值，$n$是正整数，$m$是质量。

有限位势垒

主条目：有限位势垒和量子穿隧效应

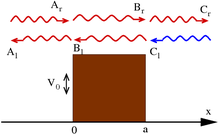
对于一个垒高为 V₀ 的位势垒的散射。往左与往右的量子波的波幅与方向都分别表示于图内。用来计算透射系数与反射系数的量子波都以红色表示

在1D情况下，粒子处于如下势垒中：

$V(x)={\begin{cases}V_{0}&|x|<a\\0&{\text{otherwise,}}\end{cases}}$

其波函数的定态解为($k,\kappa$为常数)

$\psi (x)={\begin{cases}A_{\mathrm {r} }\exp(ikx)+A_{\mathrm {l} }\exp(-ikx)&x<-a,\\B_{\mathrm {r} }\exp(\kappa x)+B_{\mathrm {l} }\exp(-\kappa x)&|x|\leq a,\\C_{\mathrm {r} }\exp(ikx)+C_{\mathrm {l} }\exp(-ikx)&x>a.\end{cases}}$

量子点

量子点中3D受束缚的电子波函数。如图所示为方形和三角形量子点。方形量子点中的电子态更像s轨道和p轨道。然而，由于不同的几何形态导致不同的束缚，三角形量子点中的波函数则是多种轨道混合的结果。

量子点是在把激子在三个空间方向上束缚住的半导体纳米结构。粒子在三个方向上都处在势阱中。势阱可以由于静电势（由外部的电极，掺杂，应变，杂质产生），两种不同半导体材料的界面（例如：在自组量子点中），半导体的表面（例如：半导体纳米晶体），或者以上三者的结合。量子点具有分离的量子化的能谱。所对应的波函数在空间上位于量子点中，但延伸于数个晶格周期中。其中的能级可以用类似无限深方形阱的模型来描述，能级位置取决于势阱宽度。

参阅

• 波包