| 名称
|
函数图形
|
方程式
|
导数
|
区间
|
连续性[1]
|
单调
|
一阶导数单调
|
原点近似恒等
|
| 恒等函数
|

|

|

|

|

|
是
|
是
|
是
|
| 单位阶跃函数
|

|

|

|

|

|
是
|
否
|
否
|
| 逻辑函数 (S函数的一种)
|

|
 [2] [2]
|

|

|

|
是
|
否
|
否
|
| 双曲正切函数
|

|

|

|

|

|
是
|
否
|
是
|
| 反正切函数
|

|

|

|

|

|
是
|
否
|
是
|
| Softsign 函数[1][2]
|

|

|

|

|

|
是
|
否
|
是
|
| 反平方根函数 (ISRU)[3]
|

|

|

|

|

|
是
|
否
|
是
|
| 线性整流函数 (ReLU)
|

|

|

|

|

|
是
|
是
|
否
|
| 带泄露线性整流函数 (Leaky ReLU)
|

|

|

|

|

|
是
|
是
|
否
|
| 参数化线性整流函数 (PReLU)[4]
|

|

|

|

|

|
Yes iff 
|
是
|
Yes iff 
|
| 带泄露随机线性整流函数 (RReLU)[5]
|

|
 [3] [3]
|

|

|

|
是
|
是
|
否
|
| 指数线性函数 (ELU)[6]
|

|

|

|

|

|
Yes iff 
|
Yes iff 
|
Yes iff 
|
| 扩展指数线性函数 (SELU)[7]
|
|

with  and and 
|

|

|

|
是
|
否
|
否
|
| S 型线性整流激活函数 (SReLU)[8]
|
|

 are parameters. are parameters.
|

|

|

|
否
|
否
|
否
|
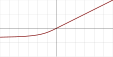
| 反平方根线性函数 (ISRLU)[3]
|
|

|

|

|

|
是
|
是
|
是
|
| 自适应分段线性函数 (APL)[9]
|
|

|
 [4] [4]
|

|

|
否
|
否
|
否
|
| SoftPlus 函数[10]
|

|

|

|

|

|
是
|
是
|
否
|
| 弯曲恒等函数
|

|

|

|

|

|
是
|
是
|
是
|
| S 型线性加权函数 (SiLU)[11] (也被称为Swish[12])
|
|
 [5] [5]
|
 [6] [6]
|

|

|
否
|
否
|
否
|
| 软指数函数[13]
|

|

|

|

|

|
是
|
是
|
Yes iff 
|
| 正弦函数
|

|

|

|
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
|

|
否
|
否
|
是
|
| Sinc 函数
|

|

|

|
![{\displaystyle [\approx -0.217234,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e0f03c0238da416a71a0c70d8f234ab5b2be365)
|

|
否
|
否
|
否
|
| 高斯函数
|

|

|

|
![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4)
|

|
否
|
否
|
否
|



















 [cs.LG].
[cs.LG].
 [cs.CV].
[cs.CV].
 [cs.LG].
[cs.LG].
 [cs.LG].
[cs.LG].
 [cs.LG].
[cs.LG].
 [cs.CV].
[cs.CV].
 [cs.NE].
[cs.NE].
 .
.
 .
.


































































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)


![{\displaystyle [\approx -0.217234,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e0f03c0238da416a71a0c70d8f234ab5b2be365)


![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4)







