動力系統理論
動力系統理論(英語:Dynamical Systems Theory),是數學領域中的一部份.主要在描述複雜的動力系統,一般會用微分方程或差分方程來表示。若用微分方程來表示,會稱為「連續動態系統」,若用差分方程來表示,則稱為「離散動態系統」。若其時間只在一些特定區域連續,在其餘區域離散,或時間是任意的時間集合(像康托爾集),需要用時標微積分來處理。有時也會需要用混合的算子來處理,像微分差分方程。
動態系統理論處理動態系統長期的量化特性.及研究一些自然界基本的運動方程系統的解,包括衛星的運動方程,電路的特性.以及生物學中出現偏微分方程的解。許多當代的研究集中在混沌理論的研究。
此領域有時也稱為動力系統、系統理論、數學動態系統理論或是動態系統的數學理論等。
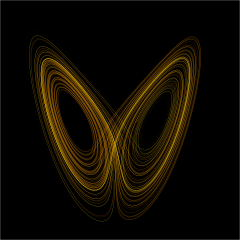
簡介
[編輯]動力系統理論處理動力系統長期的量化特性,因此其重點一般不是找出描述動態系統方程式的精確解(多半也很難找到精確解),而是希望可以回答類似以下的問題:「系統會收斂到一個穩定狀態嗎?若會的話,其穩定狀態是什麼?」或是「其長期特性和系統的初始值有關嗎?」
動態系統理論的重要目的是要找到動態系統的不動點或是穩態,也就是一些使系統狀態可以維持定值,不隨時間改變的數值。有些不動點稱為吸引子,是指若系統的初始值在這些點附近,系統會慢慢趨近吸引子。
另一個常見的是周期點,是指系統狀態在若干時間之後會重複先前的狀態。週期點也可能是吸引子。沙可夫斯基定理是一個有趣的定理.和一維離散動態系統的週期點個數有關。
即使是簡單的非線性動態系統,也會出現看似隨機的,完全無法預測的情形,此情形稱為混沌。動力系統理論中的混沌理論會為混沌有清楚定義及分析其特性。
歷史
[編輯]動態系統理論的概念起源自牛頓力學,如同其他自然科學及工程法則一様,動態系統是找出系統此一時刻的狀態和未來狀態之間的關係。
在電腦發明之前,求解動態系統需要複雜的數學技巧,而且可能只能求解某些特定的動態系統。
概念
[編輯]動態系統
[編輯]動態系統的概念是一個固定規則的數學形式系統,而此規則可用來描述一個點的位置和其環繞空間的時間相依性。例如描述單擺擺動的數學模型、描述管子中水流的數學模型、以及描述每年春天湖中魚類數量的數學模型。
動態系統有由一組實數組成的狀態,或更普遍的是在適當狀態空間中點的集合。系統狀態的微小變化對應這些數值的微小變動。這些數也是一個幾何空間(流形)的座標。動態系統的演化定律是一個描述如何由現在狀態轉變為未來狀態的函數。此函數是確定性的,若目前狀態不變,在特定未來時間下只會有一種狀態。
動態性
[編輯]動態性也稱為「動態假說」、「認知科學的動態假說」或「動態認知」,是由哲學家馮·蓋爾德提出的的認知科學新領域。動態假說認為微分方程比傳統的電腦模型更適合為認知建模。
非線性系統
[編輯]數學上的非線性系統是指不滿足疊加原理的系統。若動態系統為線性系統,則系統方程任意兩個解的線性疊加仍然是方程的一個解。但非線性系統沒有這項特性,因此在求解上會比較困難。
相關領域
[編輯]算術動態系統
[編輯]算術動態系統是在1990年代提出的數學理論.整合了動態系統及數論。傳統的離散動態系統會探討迭代函數在複數平面或是實數中的性質。算術動態系統是探討多項式或有理函數在整數、有理數、p進數及幾何點中的迭代特性。
混沌理論
[編輯]混沌理論是描述一些特定動態系統的特性,這些動態系統的狀態會隨時間而變化,而且和對其初始狀態有高度的敏感性(稱為蝴蝶效應),由於初始狀態的微擾會使狀態的誤差隨著時間呈指數的成長,因此混沌系統看似是隨機,但其實混沌系統是一個確定系統,其未來的動態特性是由初始狀態所完全決定,沒有隨機的因素在內。
複雜系統
[編輯]複雜系統是一門研究自然、社會及科學中有複雜特性系統的共通點,也稱為「複雜系統理論」、「複雜科學」或「複雜系統研究」。這些系統的主要問題是他們難以建模及模擬。以這個觀點來看,不同的研究文本會依不同的屬性定義何為複雜系統。
在許多科學領域中.化約論的策略己無法適用,複雜系統的研究為這些領域帶來新的活力。複雜系統常用來作為一個廣義的詞語,用在不同的學科中,包括神經科學、社會科學、氣象學、物理、化學、電腦科學、心理學、人工生命、進化計算、地震預測、分子生物學等。
控制理論
[編輯]控制理論是工程學與數學的跨領域分支,其主要處理動態系統的行為。
遍歷理論
[編輯]遍歷理論是研究有不變測度的動態系統及其相關問題的一個數學分支。遍歷理論的發展一開始是因為統計物理中的問題。
泛函分析
[編輯]泛函分析是數學中數學分析的一個分支,主要在研究向量空間在作用在其中的運算子。泛函分析源自函數空間的研究,特別是一些函數的轉換(像是傅立葉轉換)以及有關微分方程及積分方程的研究。「泛函」一詞是來自變分學,是指一個輸入值也是函數的函數,泛函一詞是由數學家斯特凡·巴拿赫所創,因著數學家及物理家維多·沃爾泰拉而廣為人知。
圖動態系統
[編輯]圖動態系統(GDS)的概念可用在許多發生在圖及網路上的過程。在圖動態系統的數學分析及電腦分析中.主要的是其結構性質(網路連接性)及其產生的動態。
投影動力系統
[編輯]投影動力系統探討一個解限制在一個拘束集合中的動態系統。這領域和最佳化及平衡問題中的靜態特性有關,也和常微分方程中的動態特性有關,且會同時應用到上述二者的特質。投影動力系統是由投影微分方程的流所決定。
符號動力學
[編輯]符號動力學是將一個拓撲或光滑的動態系統用一個離散空間來建模,而離散空間包括了抽象符號組成的無窮序列,其中每一個符號對應了系統的一個狀態,而其動態是由位移運算符來產生。
系統動力學
[編輯]系統動力學是研究複雜系統隨著時間的變化,其中也研究內在的反饋迴路及時間延遲等會影響整個系統特性的因素[1]。系統動力學和其他研究複雜系統方法的不同處是使用反饋迴路及存量和流量的概念,這些元素有助於說明為何看似簡單的系統會出現難以理解的非線性。
拓撲動力學
[編輯]拓撲動力學是以點集拓撲學的觀點來研究動態系統的質化特性及漸近特性。
應用
[編輯]生物學
[編輯]在運動生物力學中,運動科學和動態系統理論結合,成為一個運動表現1建模的可行框架。以動態系統的觀點來看,人類的運動系統是一個高度複雜的系統,由許多彼此相關的子系統構成(如呼吸系統、循環系統、骨骼肌肉系統及知覺系統),而各子系統又是由大量彼此相關的組件(像血球、氧分子、肌肉組織、代謝酶,結締組織和骨)所構成。在動態系統理論中,運動模型融合了這些物理系統及生物系統中自組織的過程[2]。
認知科學
[編輯]動態系統理論已應用在神經動力學及認知科學中,尤其是在新皮亞傑學派。此學派認為認知科學最適合用物理理論來表示.而不是用以語法學及人工智慧為基礎的理論,此學派也認為微分方程是最適合為人類行為建模的數學工具,可以表示在狀態空間中的認知軌跡。換句話說.此學派認為心理學應該是描述人在特定環境及內在壓力下的認知及反應(並且是用微分方程來描述),其中也常用到混沌理論來描述[3]。
在動態系統理論中,當舊的學習模式被破壞時.學習者的心智會到一個不平衡的狀態,即為認知發展的相變期,活動水平會以自組織的方式互相連結,新形成的微觀及巨觀結構互相支持,加速形成的過程。新的狀態是漸進的,離散的,異質的及不可預測的[4]。
近來動態系統理論也用來解釋A非B錯誤,是兒童發展學中一個長久未能解答的問題[5]。
相關條目
[編輯]參考資料
[編輯]- ^ MIT System Dynamics in Education Project (SDEP). [2017-06-22]. (原始內容存檔於2008-05-09).
- ^ Paul S Glaziera, Keith Davidsb, Roger M Bartlettc (2003). "DYNAMICAL SYSTEMS THEORY: a Relevant Framework for Performance-Oriented Sports Biomechanics Research" (頁面存檔備份,存於網際網路檔案館). in: Sportscience 7. Accessdate=2008-05-08.
- ^ 陳仁祥. 混沌、認知、生理學. 科學月刊1995年5月304期. [2013-08-21]. (原始內容存檔於2013-08-27).
- ^ Lewis, Mark D. The Promise of Dynamic Systems Approaches for an Integrated Account of Human Development (PDF). Child Development. 2000-02-25, 71 (1): 36–43 [2008-04-04]. PMID 10836556. doi:10.1111/1467-8624.00116. (原始內容 (PDF)存檔於2022-03-01).
- ^ Smith, Linda B.; Esther Thelen. Development as a dynamic system (PDF). TRENDS in Cognitive Sciences. 2003-07-30, 7 (8): 343–8 [2008-04-04]. doi:10.1016/S1364-6613(03)00156-6. (原始內容 (PDF)存檔於2019-07-11).
延伸閱讀
[編輯]- Abraham, Frederick D.; Abraham, Ralph; Shaw, Christopher D. A Visual Introduction to Dynamical Systems Theory for Psychology. Aerial Press. 1990. ISBN 978-0-942344-09-7. OCLC 24345312.
- Beltrami, Edward J. Mathematics for Dynamic Modeling 2nd. Academic Press. 1998. ISBN 978-0-12-085566-7. OCLC 36713294.
- Hájek, Otomar. Dynamical systems in the plane. Academic Press. 1968. OCLC 343328.
- Luenberger, David G. Introduction to dynamic systems: theory, models, and applications. Wiley. 1979. ISBN 978-0-471-02594-8. OCLC 4195122.
- Michel, Anthony; Kaining Wang; Bo Hu. Qualitative Theory of Dynamical Systems. Taylor & Francis. 2001. ISBN 978-0-8247-0526-8. OCLC 45873628.
- Padulo, Louis; Arbib, Michael A. System theory: a unified state-space approach to continuous and discrete systems. Saunders. 1974. ISBN 9780721670355. OCLC 947600.
- Strogatz, Steven H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Addison Wesley. 1994. ISBN 978-0-7382-0453-6. OCLC 49839504.
外部連結
[編輯]- Dynamic Systems Encyclopedia of Cognitive Science entry.
- Definition of dynamical system(頁面存檔備份,存於網際網路檔案館) in MathWorld.
- DSWeb(頁面存檔備份,存於網際網路檔案館) Dynamical Systems Magazine

