半精度浮點數
外觀
| 浮點數運算 計算機數值編碼 |
|---|
| IEEE 754 |
| 其它 |
| 高精度計算 |
半精度浮點數 是一種被計算機使用的二進制浮點數據類型。半精度浮點數使用2個字節(16位)來存儲。
在IEEE 754-2008中,它被稱作binary16。這種數據類型只適合存儲對精度要求不高的數字,不適合用來計算。
半精度浮點數是一種較新的浮點類型。 英偉達在2002年初發布的Cg語言中稱它作 half 類型,並首次在2002年末發布的GeForce FX中實現。[1]ILM 當時正在尋找一種擁有高動態範圍,且不需過多消耗硬盤和內存,並且能像單精度浮點數和雙精度浮點數那樣被用來進行浮點計算的圖像格式。[2]由SGI的John Airey領導的硬件加速可編程着色小組在1997年發明了作為'bali'設計工作的一部分的s10e5數據類型,曾在SIGGRAPH 2000年的論文[3]中介紹過。(見章節 4.3)並且在美國專利7518615[4]中被進一步記錄。
半精度浮點數可在OpenEXR, JPEG XR, OpenGL, Cg語言、D3DX等計算機圖形環境中使用。其與8位或16位整數相比具有動態範圍高的優點,可以使高對比度圖片中更多細節得以保留。與單精度浮點數相比,它的優點是只需要一半的存儲空間和帶寬(但是會犧牲精度和數值範圍)。[2]
定義
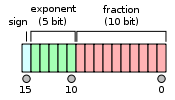
[編輯]IEEE 754 標準指定了一個 binary16 要有如下的格式:
- Sign bit(符號位): 1 bit
- Exponent width(指數位寬): 5 bits
- Significand precision(尾數精度): 11 bits (有10位被顯式存儲)
按如下順序排列:
除非指數位全是0,否則就會假定隱藏的起始位是1。因此只有10位尾數在內存中被顯示出來,而總精度是11位。據IEEE 754的說法,雖然尾數只有10位,但是尾數精度是11位的(log10(211) ≈ 3.311 十進制數).
例子
[編輯]0 01111 0000000000 = 1 0 01111 0000000001 = 1 + 2−10 = 1.0009765625 (1之后的最接近的数) 1 10000 0000000000 = −2 0 11110 1111111111 = 65504 (max half precision) 0 00001 0000000000 = 2−14 ≈ 6.10352 × 10−5 (最小正指数) 0 00000 1111111111 = 2−14 - 2−24 ≈ 6.09756 × 10−5 (最大尾数) 0 00000 0000000001 = 2−24 ≈ 5.96046 × 10−8 (最小正尾数) 0 00000 0000000000 = 0 1 00000 0000000000 = −0 0 11111 0000000000 = infinity 1 11111 0000000000 = −infinity 0 01101 0101010101 = 0.333251953125 ≈ 1/3
由於尾數的位數是奇數,所以默認情況下,1/3 這類的數會像雙精度浮點數一樣四捨五入。
參閱
[編輯]- IEEE 754: IEEE二進制浮點數算數標準 (IEEE 754)
- ISO/IEC 10967, Language Independent Arithmetic
- Primitive data type
- RGBE image format
引用
[編輯]外部連結
[編輯]- Minifloats(頁面存檔備份,存於網際網路檔案館) (in Survey of Floating-Point Formats)
- OpenEXR site(頁面存檔備份,存於網際網路檔案館)
- Half precision constants(頁面存檔備份,存於網際網路檔案館) from D3DX
- OpenGL treatment of half precision
- Fast Half Float Conversions[失效連結]
- Analog devices variant(頁面存檔備份,存於網際網路檔案館) (four-bit exponent)
- C source code to convert between IEEE double, single, and half precision can be found here(頁面存檔備份,存於網際網路檔案館)
- C# source code implementing a half-precision floating-point data type can be found here[永久失效連結]
- Java source code for half-precision floating-point conversion
- Half precision floating point for one of the extended GCC features(頁面存檔備份,存於網際網路檔案館)
- [1](頁面存檔備份,存於網際網路檔案館)