在集合論和數學的其他分支中,存在差集的兩種定義:相對差集(差集)和絕對差集(補集)。
 相對補集
相對補集
若 和
和 是集合,則
是集合,則 在
在 中的相對差集(簡稱差集)是由所有屬於
中的相對差集(簡稱差集)是由所有屬於 但不屬於
但不屬於 的元素組成的集合。
的元素組成的集合。
 在
在 中的相對補集記為
中的相對補集記為 或
或 。
。
形式上:

例如:


- 若
 是實數集合,
是實數集合, 是有理數集合,則
是有理數集合,則 為無理數集合。
為無理數集合。
下列命題給出一些相對補集同併集和交集等集合論運算相關的一些常用性質。
命題1:若 是集合,則下列等式恆成立:
是集合,則下列等式恆成立:








 絕對補集
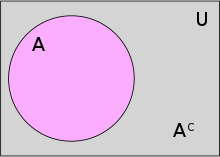
絕對補集
若給定全集 ,則
,則 在
在 中的相對補集稱為
中的相對補集稱為 的絕對差集(又稱為補集),記為
的絕對差集(又稱為補集),記為 ,即:
,即:

(注意:根據ISO與中華人民共和國國家標準, 中子集
中子集 的補集記作
的補集記作 。)
。)
例如,若全集為自然數集合,則奇數集合的補集為偶數集合。
下列命題給出一些絕對補集同併集和交集等集合論運算相關的一些重要性質。
命題2:若 和
和 是全集
是全集 的子集,則下列恆等式成立:
的子集,則下列恆等式成立:
- 德摩根定律:


- 補集律:




- 對合:

- 相對補集和絕對補集的關係:


上述表明,若 為
為 的非空子集,則
的非空子集,則 是
是 的一個分割。
的一個分割。
補集的符號在Unicode中為數學運算符區段中的「∁」(Unicode:U+2201)。





































