圖1 貝塞爾函數的一個實例:一個緊繃的鼓面在中心受到敲擊後的二階振動振型,其振幅沿半徑方向上的分布就是一個貝塞爾函數(考慮正負號)。實際生活中受敲擊的鼓面的振動是各階類似振動形態的疊加。貝塞爾函數 (Bessel functions ),是數學上的一類特殊函數 的總稱。通常單說的貝塞爾函數 指第一類貝塞爾函數 Bessel function of the first kind )。一般貝塞爾函數是下列常微分方程 (一般稱為貝塞爾方程 )的標準解函數
y
(
x
)
{\displaystyle y(x)}
x
2
d
2
y
d
x
2
+
x
d
y
d
x
+
(
x
2
−
α
2
)
y
=
0
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+(x^{2}-\alpha ^{2})y=0}
該方程的通解無法用初等函數 表示。
由於貝塞爾微分方程是二階常微分方程 ,需要由兩個獨立的函數來表示其標準解函數。典型的是使用第一類貝塞爾函數 和第二類貝塞爾函數 來表示標準解函數:
y
(
x
)
=
c
1
J
α
(
x
)
+
c
2
Y
α
(
x
)
{\displaystyle y(x)=c_{1}J_{\alpha }(x)+c_{2}Y_{\alpha }(x)}
注意,由於
Y
α
(
x
)
{\displaystyle Y_{\alpha }(x)}
發散 的(無窮 ),當取 x=0 時,相關係數
c
2
{\displaystyle c_{2}}
貝塞爾函數的具體形式隨上述方程中任意實數或複數α變化而變化(相應地,α被稱為其對應貝塞爾函數的階數 整數 n ,對應解稱為n 階貝塞爾函數
儘管在上述微分方程中,α本身的正負號不改變方程的形式,但實際應用中仍習慣針對α和−α定義兩種不同的貝塞爾函數(這樣做能帶來好處,比如消除了函數在α=0 點的不光滑性)。
貝塞爾函數也被稱為柱諧函數 圓柱函數 或圓柱諧波 ,因為他們是於拉普拉斯方程 在圓柱坐標 上的求解過程中被發現的。
貝塞爾函數的幾個正整數階特例早在18世紀中葉就由瑞士 數學家 丹尼爾·伯努利 在研究懸鏈振動時提出了,當時引起了數學界的興趣。丹尼爾 的叔叔雅各布·伯努利 ,歐拉 、拉格朗日 等數學大師對貝塞爾函數的研究作出過重要貢獻。1817年,德國 數學家貝塞爾 在研究開普勒 提出的三體引力 系統的運動問題時,第一次系統地提出了貝塞爾函數的總體理論框架,後人以他的名字來命名了這種函數 [1] [2] (頁面存檔備份 ,存於網際網路檔案館 )。
貝塞爾方程是在圓柱坐標 或球坐標 下使用分離變量法 求解拉普拉斯方程 和亥姆霍茲方程 時得到的(在圓柱域問題中得到的是整階 形式 α = n ;在球形域問題中得到的是半奇數階 形式 α = n +½),因此貝塞爾函數在波的傳播 問題以及各種涉及有勢場 的問題中占有非常重要的地位,最典型的問題有:
在其他一些領域,貝塞爾函數也相當有用。譬如在ttf字體文件壓縮,信號處理 中的調頻合成 凱澤窗 的定義中,都要用到貝塞爾函數。
貝塞爾方程是一個二階常微分方程,必然存在兩個線性無關 的解。針對各種具體情況,人們提出了表示這些解的不同形式。下面分別介紹這些不同類型的貝塞爾函數。
圖2 0階、1階和2階第一類貝塞爾函數(貝塞爾J函數)曲線第一類貝塞爾函數 (Bessel function of the first kind ),又稱貝塞爾函數 (Bessel function ),下文中有時會簡稱為J函數 ,記作J α
第一類α階貝塞爾函數J α (x )是貝塞爾方程當α為整數或α非負時的解,須滿足在x = 0 時有限。這樣選取和處理J α 的原因見本主題下面的性質介紹 ;另一種定義方法是通過它在x = 0 點的泰勒級數 展開(或者更一般地通過冪級數 展開,這適用於α為非整數):
J
α
(
x
)
=
∑
m
=
0
∞
(
−
1
)
m
m
!
Γ
(
m
+
α
+
1
)
(
x
2
)
2
m
+
α
{\displaystyle J_{\alpha }(x)=\sum _{m=0}^{\infty }{\frac {(-1)^{m}}{m!\Gamma (m+\alpha +1)}}{\left({\frac {x}{2}}\right)}^{2m+\alpha }}
上式中
Γ
(
z
)
{\displaystyle \Gamma (z)}
Γ函數 (它可視為階乘 函數向非整型自變量 的推廣)。第一類貝塞爾函數的形狀大致與按
1
/
x
{\displaystyle 1/{\sqrt {x}}}
正弦 或餘弦 函數類似(參見本頁下面對它們漸近形式的介紹),但它們的零點並不是周期性的,另外隨着x 的增加,零點的間隔會越來越接近周期性。圖2所示為0階、1階和2階第一類貝塞爾函數
J
α
(
x
)
{\displaystyle J_{\alpha }(x)}
α
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
如果α不為整數,則
J
α
(
x
)
{\displaystyle J_{\alpha }(x)}
J
−
α
(
x
)
{\displaystyle J_{-\alpha }(x)}
解系 。反之若
α
{\displaystyle \alpha }
J
−
α
(
x
)
=
(
−
1
)
α
J
α
(
x
)
{\displaystyle J_{-\alpha }(x)=(-1)^{\alpha }J_{\alpha }(x)\,}
於是兩函數之間已不滿足線性無關條件。為尋找在此情況下微分方程與
J
α
(
x
)
{\displaystyle J_{\alpha }(x)}
第二類貝塞爾函數 ,定義過程將在後面的小節中給出。
α
{\displaystyle \alpha }
J
α
(
x
)
=
1
2
π
∫
0
2
π
cos
(
α
τ
−
x
sin
τ
)
d
τ
.
{\displaystyle J_{\alpha }(x)={\frac {1}{2\pi }}\int _{0}^{2\pi }\cos(\alpha \tau -x\sin \tau )d\tau .}
(
α
{\displaystyle \alpha }
參考文獻[2] 第360頁)
這個積分式就是貝塞爾當年提出的定義,而且他還從該定義中推出了函數的一些性質。另一種積分表達式為:
J
α
(
x
)
=
1
2
π
∫
−
π
π
e
i
(
α
τ
−
x
sin
τ
)
d
τ
{\displaystyle J_{\alpha }(x)={\frac {1}{2\pi }}\int _{-\pi }^{\pi }e^{i(\alpha \tau -x\sin \tau )}d\tau }
貝塞爾函數可以用超幾何級數 表示成下面的形式:
J
α
(
z
)
=
(
z
/
2
)
α
Γ
(
α
+
1
)
0
F
1
(
α
+
1
;
−
z
2
/
4
)
.
{\displaystyle J_{\alpha }(z)={\frac {(z/2)^{\alpha }}{\Gamma (\alpha +1)}}\;_{0}F_{1}(\alpha +1;-z^{2}/4).}
ɑ為整數。由於函數線性相關的特性(用了一個就少了一個,所以要再構造一個),才需定義如下詳細介紹的第二類貝塞爾函數。
圖3 0階、1階和2階第二類貝塞爾函數(貝塞爾Y 函數)曲線圖第二類貝塞爾函數 (Bessel function of the second kind ),又稱諾伊曼函數 (Neumann function ),下文中有時會簡稱為Y函數 ,記作Y α
第二類貝塞爾函數也許比第一類更為常用。
這種函數通常用Y α (x )表示,它們是貝塞爾方程的另一類解。x = 0 點是第二類貝塞爾函數的(無窮)奇點。
Y α (x )又被稱為諾依曼函數 (Neumann function),有時也記作N α (x )。它和J α (x )存在如下關係:
Y
α
(
x
)
=
J
α
(
x
)
cos
(
α
π
)
−
J
−
α
(
x
)
sin
(
α
π
)
,
{\displaystyle Y_{\alpha }(x)={\frac {J_{\alpha }(x)\cos(\alpha \pi )-J_{-\alpha }(x)}{\sin(\alpha \pi )}},}
若α為整數(此時上式是
0
0
{\displaystyle {\frac {0}{0}}}
未定式 )則取右端的極限 值。
從前面對J α (x )的定義可以知道,若α不為整數時,定義Y α 是多餘的(因為貝塞爾方程的兩個線性無關解都已經用J函數表示出來了)。另一方面,若α為整數,Y α J α
Y
−
n
(
x
)
=
(
−
1
)
n
Y
n
(
x
)
{\displaystyle Y_{-n}(x)=(-1)^{n}Y_{n}(x)\,}
J α (x )和Y α (x )均為沿負實半軸割開的複平面 內關於x 的全純函數 。當α為整數時,複平面內不存在貝塞爾函數的支點 ,所以J 和Y 均為x 的整函數 。若將x 固定,則貝塞爾函數是α的整函數。圖3所示為0階、1階和2階第二類貝塞爾函數
Y
α
(
x
)
{\displaystyle Y_{\alpha }(x)}
α
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
第三類貝塞爾函數 (Bessel function of the third kind ),又稱漢克爾函數 (Hankel function )。
貝塞爾方程的另外一對重要的線性無關解稱為漢克爾 函數H α (1) (x )和H α (2) (x ),分別定義為:
H
α
(
1
)
(
x
)
=
J
α
(
x
)
+
i
Y
α
(
x
)
{\displaystyle H_{\alpha }^{(1)}(x)=J_{\alpha }(x)+iY_{\alpha }(x)}
H
α
(
2
)
(
x
)
=
J
α
(
x
)
−
i
Y
α
(
x
)
{\displaystyle H_{\alpha }^{(2)}(x)=J_{\alpha }(x)-iY_{\alpha }(x)}
其中i 為虛數 單位
−
1
{\displaystyle {\sqrt {-1}}}
第三類貝塞爾函數 ;它們描述了二維波動方程 的外向行柱面波 解和內向行柱面波 解("行"與在"行動"中同音)。
利用前面推出的關係可將漢克爾函數表示成:
H
α
(
1
)
(
x
)
=
J
−
α
(
x
)
−
e
−
α
π
i
J
α
(
x
)
i
sin
(
α
π
)
{\displaystyle H_{\alpha }^{(1)}(x)={\frac {J_{-\alpha }(x)-e^{-\alpha \pi i}J_{\alpha }(x)}{i\sin(\alpha \pi )}}}
H
α
(
2
)
(
x
)
=
J
−
α
(
x
)
−
e
α
π
i
J
α
(
x
)
−
i
sin
(
α
π
)
{\displaystyle H_{\alpha }^{(2)}(x)={\frac {J_{-\alpha }(x)-e^{\alpha \pi i}J_{\alpha }(x)}{-i\sin(\alpha \pi )}}}
若α為整數,則須對等號右邊取極限值。另外,無論α是不是整數,下面的關係都成立:
H
−
α
(
1
)
(
x
)
=
e
α
π
i
H
α
(
1
)
(
x
)
{\displaystyle H_{-\alpha }^{(1)}(x)=e^{\alpha \pi i}H_{\alpha }^{(1)}(x)}
H
−
α
(
2
)
(
x
)
=
e
−
α
π
i
H
α
(
2
)
(
x
)
{\displaystyle H_{-\alpha }^{(2)}(x)=e^{-\alpha \pi i}H_{\alpha }^{(2)}(x)}
貝塞爾函數當變量x 為複數 時同樣成立,並且當x 為純虛數 時能得到一類重要情形——它們被稱為第一類修正貝塞爾函數 (modified Bessel function of the first kind )和第二類修正貝塞爾函數 (modified Bessel function of the second kind ),或虛變量的貝塞爾函數 (有時還稱為雙曲型貝塞爾函數 ),定義為:
I
α
(
x
)
=
i
−
α
J
α
(
i
x
)
{\displaystyle I_{\alpha }(x)=i^{-\alpha }J_{\alpha }(ix)\!}
K
α
(
x
)
=
π
2
I
−
α
(
x
)
−
I
α
(
x
)
sin
(
α
π
)
=
π
2
i
α
+
1
H
α
(
1
)
(
i
x
)
{\displaystyle K_{\alpha }(x)={\frac {\pi }{2}}{\frac {I_{-\alpha }(x)-I_{\alpha }(x)}{\sin(\alpha \pi )}}={\frac {\pi }{2}}i^{\alpha +1}H_{\alpha }^{(1)}(ix)\!}
以上形式保證了當變量x 為實數 時,函數值亦為實數。這兩個函數構成了下列修正貝塞爾方程 (與一般貝塞爾方程的差別僅在兩個正負號)的一個相互線性無關的解系:
x
2
d
2
y
d
x
2
+
x
d
y
d
x
−
(
x
2
+
α
2
)
y
=
0.
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}-(x^{2}+\alpha ^{2})y=0.}
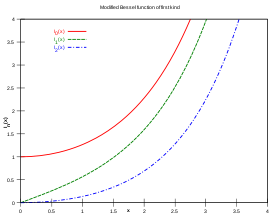
修正貝塞爾函數與一般貝塞爾函數的差別在於:一般貝塞爾函數隨實變量是振盪型的,而修正貝塞爾函數I α 和K α 則分別是指數增長 和指數衰減 型的。和第一類貝塞爾函數J α 一樣,函數I α 當α > 0 時在x =0 點等於0,當α=0時在x =0 點趨於有限值。類似地,K α 在x =0 點發散(趨於無窮)。
圖4-1 第一類修正貝塞爾函數
I
α
(
x
)
{\displaystyle I_{\alpha }(x)}
α
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
圖4-2 第二類修正貝塞爾函數
K
α
(
x
)
{\displaystyle K_{\alpha }(x)}
α
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
複數變量的貝塞爾函數之零值 :
J
α
(
x
)
=
0
{\displaystyle J_{\alpha }(x)=0}
參考文獻[5] )。
第二類修正貝塞爾函數有時候被稱為第三類修正貝塞爾函數 (modified Bessel function of the third kind )。
圖5-1 第一類球貝塞爾函數
j
n
(
x
)
{\displaystyle j_{n}(x)}
n
=
0
,
1
,
2
{\displaystyle n=0,1,2}
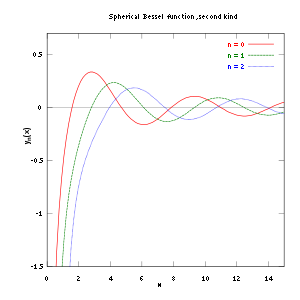
圖5-2 第二類球貝塞爾函數
y
n
(
x
)
{\displaystyle y_{n}(x)}
n
=
0
,
1
,
2
{\displaystyle n=0,1,2}
若使用分離變量法 求解球坐標 下的三維亥姆霍茲方程 ,則可得到如下形式關於徑向(r 方向)分量的常微分方程 :
x
2
d
2
y
d
x
2
+
2
x
d
y
d
x
+
[
x
2
−
n
(
n
+
1
)
]
y
=
0.
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+2x{\frac {dy}{dx}}+[x^{2}-n(n+1)]y=0.}
關於上述方程的一對線性無關解稱為球貝塞爾函數 ,分別用j n y n n n J n Y n
j
n
(
x
)
=
π
2
x
J
n
+
1
/
2
(
x
)
,
{\displaystyle j_{n}(x)={\sqrt {\frac {\pi }{2x}}}J_{n+1/2}(x),}
y
n
(
x
)
=
π
2
x
Y
n
+
1
/
2
(
x
)
=
(
−
1
)
n
+
1
π
2
x
J
−
n
−
1
/
2
(
x
)
.
{\displaystyle y_{n}(x)={\sqrt {\frac {\pi }{2x}}}Y_{n+1/2}(x)=(-1)^{n+1}{\sqrt {\frac {\pi }{2x}}}J_{-n-1/2}(x).}
球貝塞爾函數也可寫成:
j
n
(
x
)
=
(
−
x
)
n
(
1
x
d
d
x
)
n
sin
x
x
,
{\displaystyle j_{n}(x)=(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}\,{\frac {\sin x}{x}},}
y
n
(
x
)
=
−
(
−
x
)
n
(
1
x
d
d
x
)
n
cos
x
x
.
{\displaystyle y_{n}(x)=-(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}\,{\frac {\cos x}{x}}.}
0階第一類球貝塞爾函數
j
0
(
x
)
{\displaystyle j_{0}(x)}
sinc函數 。頭幾階整階球貝塞爾函數的表達式分別為:
第一類:
j
0
(
x
)
=
sin
x
x
{\displaystyle j_{0}(x)={\frac {\sin x}{x}}}
j
1
(
x
)
=
sin
x
x
2
−
cos
x
x
{\displaystyle j_{1}(x)={\frac {\sin x}{x^{2}}}-{\frac {\cos x}{x}}}
j
2
(
x
)
=
(
3
x
2
−
1
)
sin
x
x
−
3
cos
x
x
2
{\displaystyle j_{2}(x)=\left({\frac {3}{x^{2}}}-1\right){\frac {\sin x}{x}}-{\frac {3\cos x}{x^{2}}}}
第二類:
y
0
(
x
)
=
−
j
−
1
(
x
)
=
−
cos
x
x
{\displaystyle y_{0}(x)=-j_{-1}(x)=-\,{\frac {\cos x}{x}}}
y
1
(
x
)
=
j
−
2
(
x
)
=
−
cos
x
x
2
−
sin
x
x
{\displaystyle y_{1}(x)=j_{-2}(x)=-\,{\frac {\cos x}{x^{2}}}-{\frac {\sin x}{x}}}
y
2
(
x
)
=
−
j
−
3
(
x
)
=
(
−
3
x
2
+
1
)
cos
x
x
−
3
sin
x
x
2
.
{\displaystyle y_{2}(x)=-j_{-3}(x)=\left(-\,{\frac {3}{x^{2}}}+1\right){\frac {\cos x}{x}}-{\frac {3\sin x}{x^{2}}}.}
還可以依照前面構造漢克爾函數相同的步驟構造所謂球漢克爾函數 :
h
n
(
1
)
(
x
)
=
j
n
(
x
)
+
i
y
n
(
x
)
{\displaystyle h_{n}^{(1)}(x)=j_{n}(x)+iy_{n}(x)}
h
n
(
2
)
(
x
)
=
j
n
(
x
)
−
i
y
n
(
x
)
.
{\displaystyle h_{n}^{(2)}(x)=j_{n}(x)-iy_{n}(x).}
事實上,所有半奇數階貝塞爾函數都可以寫成由三角函數 組成的封閉形式的表達式,球貝塞爾函數也同樣可以。特別地,對所有非負整數n ,存在:
h
n
(
1
)
(
x
)
=
(
−
i
)
n
+
1
e
i
x
x
∑
m
=
0
n
i
m
m
!
(
2
x
)
m
(
n
+
m
)
!
!
(
n
−
m
)
!
!
{\displaystyle h_{n}^{(1)}(x)=(-i)^{n+1}{\frac {e^{ix}}{x}}\sum _{m=0}^{n}{\frac {i^{m}}{m!(2x)^{m}}}{\frac {(n+m)!!}{(n-m)!!}}}
而對實自變量x ,h n (2) 是上面h n (1) 的復共軛(!! 表示雙階乘 )。由此我們可以通過得到h ,再分離實部虛部,求出相應階j 和h 的表達式,譬如j 0 (x ) = sin(x )/x ,y 0 (x ) = -cos(x )/x ,等等。
球貝塞爾函數的生成函數為:
1
z
cos
(
z
2
−
2
z
t
)
=
∑
n
=
0
∞
t
n
n
!
j
n
−
1
(
z
)
,
{\displaystyle {\frac {1}{z}}\cos({\sqrt {z^{2}-2zt}})=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}j_{n-1}(z),}
1
z
sin
(
z
2
−
2
z
t
)
=
∑
n
=
0
∞
t
n
n
!
y
n
−
1
(
z
)
.
{\displaystyle {\frac {1}{z}}\sin({\sqrt {z^{2}-2zt}})=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}y_{n-1}(z).}
Sn Cn ξn ζn [ 編輯 ] 黎卡提-貝塞爾函數(Riccati-Bessel functions)和球貝塞爾函數比較類似:
S
n
(
x
)
=
x
j
n
(
x
)
=
π
x
/
2
J
n
+
1
/
2
(
x
)
{\displaystyle S_{n}(x)=xj_{n}(x)={\sqrt {\pi x/2}}J_{n+1/2}(x)}
C
n
(
x
)
=
−
x
y
n
(
x
)
=
−
π
x
/
2
Y
n
+
1
/
2
(
x
)
{\displaystyle C_{n}(x)=-xy_{n}(x)=-{\sqrt {\pi x/2}}Y_{n+1/2}(x)}
ζ
n
(
x
)
=
x
h
n
(
2
)
(
x
)
=
π
x
/
2
H
n
+
1
/
2
(
2
)
(
x
)
=
S
n
(
x
)
+
i
C
n
(
x
)
{\displaystyle \zeta _{n}(x)=xh_{n}^{(2)}(x)={\sqrt {\pi x/2}}H_{n+1/2}^{(2)}(x)=S_{n}(x)+iC_{n}(x)}
該函數滿足方程:
x
2
d
2
y
d
x
2
+
[
x
2
−
n
(
n
+
1
)
]
y
=
0
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+[x^{2}-n(n+1)]y=0}
這個方程以及相應的黎卡提-貝塞爾解 是德國 物理學家 古斯塔夫·米 (Gustav Mie )於1908年研究電磁波 在球狀顆粒表面散射 問題時提出的,後人將這種散射稱為米氏散射 (Mie scattering )。這個問題近幾年的進展可參見文獻 Du (2004)。
後人有時會遵從德拜 (Debye )在1909年的論文中的記法,用
ψ
n
,
χ
n
{\displaystyle \psi _{n},\chi _{n}}
S
n
,
C
n
{\displaystyle S_{n},C_{n}}
貝塞爾函數在α非負時具有下面的漸近形式。當自變量x 為小量,即
0
<
x
≪
α
+
1
{\displaystyle 0<x\ll {\sqrt {\alpha +1}}}
J
α
(
x
)
→
1
Γ
(
α
+
1
)
(
x
2
)
α
{\displaystyle J_{\alpha }(x)\rightarrow {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {x}{2}}\right)^{\alpha }}
Y
α
(
x
)
→
{
2
π
[
ln
(
x
/
2
)
+
γ
]
if
α
=
0
−
Γ
(
α
)
π
(
2
x
)
α
if
α
>
0
{\displaystyle Y_{\alpha }(x)\rightarrow \left\{{\begin{matrix}{\frac {2}{\pi }}\left[\ln(x/2)+\gamma \right]&{\mbox{if }}\alpha =0\\\\-{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{if }}\alpha >0\end{matrix}}\right.}
式中γ為歐拉-馬歇羅尼常數 (也叫歐拉常數,等於 0.5772156649...),Γ為Γ函數 。對於很大的x ,即
x
≫
|
α
2
−
1
/
4
|
{\displaystyle x\gg |\alpha ^{2}-1/4|}
J
α
(
x
)
→
2
π
x
cos
(
x
−
α
π
2
−
π
4
)
{\displaystyle J_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\cos \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)}
Y
α
(
x
)
→
2
π
x
sin
(
x
−
α
π
2
−
π
4
)
.
{\displaystyle Y_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\sin \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right).}
(α=1/2 時漸近號兩邊嚴格相等;參見前面對球貝塞爾函數的介紹)。其他形式貝塞爾函數的漸近形式可以從上面的式子直接推得。譬如,對大自變量
x
≫
|
α
2
−
1
/
4
|
{\displaystyle x\gg |\alpha ^{2}-1/4|}
I
α
(
x
)
→
1
2
π
x
e
x
,
{\displaystyle I_{\alpha }(x)\rightarrow {\frac {1}{\sqrt {2\pi x}}}e^{x},}
K
α
(
x
)
→
π
2
x
e
−
x
.
{\displaystyle K_{\alpha }(x)\rightarrow {\sqrt {\frac {\pi }{2x}}}e^{-x}.}
對小自變量
0
<
x
≪
α
+
1
{\displaystyle 0<x\ll {\sqrt {\alpha +1}}}
I
α
(
x
)
→
1
Γ
(
α
+
1
)
(
x
2
)
α
{\displaystyle I_{\alpha }(x)\rightarrow {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {x}{2}}\right)^{\alpha }}
K
α
(
x
)
→
{
−
ln
(
x
/
2
)
−
γ
if
α
=
0
Γ
(
α
)
2
(
2
x
)
α
if
α
>
0
{\displaystyle K_{\alpha }(x)\rightarrow \left\{{\begin{matrix}-\ln(x/2)-\gamma &{\mbox{if }}\alpha =0\\\\{\frac {\Gamma (\alpha )}{2}}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{if }}\alpha >0\end{matrix}}\right.}
整階(α = n )第一類貝塞爾函數J n 母函數 generating function )的羅朗級數 (Laurent series )展開來定義:
e
(
x
/
2
)
(
t
−
1
/
t
)
=
∑
n
=
−
∞
∞
J
n
(
x
)
t
n
,
{\displaystyle e^{(x/2)(t-1/t)}=\sum _{n=-\infty }^{\infty }J_{n}(x)t^{n},}
上式得左邊即為整階第一類貝塞爾函數的母函數,這是丹麥 天文學家 漢森 於1843年提出的。(這種定義也可以通過路徑積分 或其他方法推廣到非整數階)。整階函數的另一個重要性質是下列雅可比-安格爾恆等式 (Jacobi-Anger identity ):
e
i
z
cos
ϕ
=
∑
n
=
−
∞
∞
i
n
J
n
(
z
)
e
i
n
ϕ
,
{\displaystyle e^{iz\cos \phi }=\sum _{n=-\infty }^{\infty }i^{n}J_{n}(z)e^{in\phi },}
利用這一等式可以將平面波 展開成一系列柱面波的疊加,或者將調頻 信號分解成傅里葉級數 的疊加。
函數J α 、Y α 、H α (1) 和H α (2) 均滿足遞推關係 :
Z
α
−
1
(
x
)
+
Z
α
+
1
(
x
)
=
2
α
x
Z
α
(
x
)
{\displaystyle Z_{\alpha -1}(x)+Z_{\alpha +1}(x)={\frac {2\alpha }{x}}Z_{\alpha }(x)}
Z
α
−
1
(
x
)
−
Z
α
+
1
(
x
)
=
2
d
Z
α
d
x
{\displaystyle Z_{\alpha -1}(x)-Z_{\alpha +1}(x)=2{\frac {dZ_{\alpha }}{dx}}}
其中Z 代表J , Y , H (1) 或H (2) 。(常將這兩個恆等式聯立推出其他關係)。從這組遞推關係可以通過低階貝塞爾函數(或它們的低階導數 )計算高階貝塞爾函數(或它們的高階導數 )。特別地,有:
(
d
x
d
x
)
m
[
x
α
Z
α
(
x
)
]
=
x
α
−
m
Z
α
−
m
(
x
)
{\displaystyle \left({\frac {d}{xdx}}\right)^{m}\left[x^{\alpha }Z_{\alpha }(x)\right]=x^{\alpha -m}Z_{\alpha -m}(x)}
(
d
x
d
x
)
m
[
Z
α
(
x
)
x
α
]
=
(
−
1
)
m
Z
α
+
m
(
x
)
x
α
+
m
{\displaystyle \left({\frac {d}{xdx}}\right)^{m}\left[{\frac {Z_{\alpha }(x)}{x^{\alpha }}}\right]=(-1)^{m}{\frac {Z_{\alpha +m}(x)}{x^{\alpha +m}}}}
由於貝塞爾方程對應的作用算符除以x 後便是一個(自伴隨 的)厄米算符 (Hermitian ),所以它的解在適當的邊界條件 下須滿足正交性關係。特別地,可推得:
∫
0
1
x
J
α
(
x
u
α
,
m
)
J
α
(
x
u
α
,
n
)
d
x
=
δ
m
,
n
2
J
α
+
1
(
u
α
,
m
)
2
,
{\displaystyle \int _{0}^{1}xJ_{\alpha }(xu_{\alpha ,m})J_{\alpha }(xu_{\alpha ,n})dx={\frac {\delta _{m,n}}{2}}J_{\alpha +1}(u_{\alpha ,m})^{2},}
其中α > -1,δm ,n 克羅內克δ ,u α,m 表示J α (x )的第m 級零點 。這個正交性關係可用於計算傅里葉-貝塞爾級數 中各項的係數,以利用該級數將任意函數寫成α固定、m 變化的函數J α (x u α,m )的無窮疊加形式。(可以立即得到球貝塞爾函數相應的關係)。
另一個正交性關係是下列在α > -1/2時成立的「封閉方程」(closure equation ):
∫
0
∞
x
J
α
(
u
x
)
J
α
(
v
x
)
d
x
=
1
u
δ
(
u
−
v
)
{\displaystyle \int _{0}^{\infty }xJ_{\alpha }(ux)J_{\alpha }(vx)dx={\frac {1}{u}}\delta (u-v)}
其中δ為狄拉克δ函數 。球貝塞爾函數的正交性條件為(當α > 0):
∫
0
∞
x
2
j
α
(
u
x
)
j
α
(
v
x
)
d
x
=
π
2
u
2
δ
(
u
−
v
)
{\displaystyle \int _{0}^{\infty }x^{2}j_{\alpha }(ux)j_{\alpha }(vx)dx={\frac {\pi }{2u^{2}}}\delta (u-v)}
貝塞爾方程的另一個重要性質與其朗斯基行列式 (Wronskian )相關,由阿貝爾恆等式 (Abel's identity )得到:
A
α
(
x
)
d
B
α
d
x
−
d
A
α
d
x
B
α
(
x
)
=
C
α
x
,
{\displaystyle A_{\alpha }(x){\frac {dB_{\alpha }}{dx}}-{\frac {dA_{\alpha }}{dx}}B_{\alpha }(x)={\frac {C_{\alpha }}{x}},}
其中A α 和B α 是貝塞爾方程的任意兩個解,C α 是與x 無關的常數(由α和貝塞爾函數的種類決定)。譬如,若A α = J α 、B α = Y α ,則C α is 2/π。該性質在修正貝塞爾函數中同樣適用,譬如,若A α = I α 、B α = K α ,則C α 為-1。
[1] 嚴鎮軍編,《數學物理方程》,第二版,中國科學技術大學出版社,合肥,2002,第82頁~第123頁,ISBN 7-312-00799-6
[2] Milton Abramowitz and Irene A. Stegun, eds., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (Dover: New York, 1972) (英文)
[3] George B. Arfken and Hans J. Weber, Mathematical Methods for Physicists (Harcourt: San Diego, 2001).
[4] Frank Bowman, Introduction to Bessel Functions (Dover: New York, 1958) ISBN 0-486-60462-4 .
[5] G. N. Watson, A Treatise on the Theory of Bessel Functions, Second Edition , (1966) Cambridge University Press.
[6] G. Mie, "Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen", Ann. Phys. Leipzig 25 (1908), p.377.
[7] Hong Du, "Mie-scattering calculation," Applied Optics 43 (9), 1951-1956 (2004).









































![{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+2x{\frac {dy}{dx}}+[x^{2}-n(n+1)]y=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfd13e94863668203e3a8e5078ce0a6071c95b2b)



















![{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+[x^{2}-n(n+1)]y=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7795a623edf57ced1f95d670ca137aa5521660b5)




![{\displaystyle Y_{\alpha }(x)\rightarrow \left\{{\begin{matrix}{\frac {2}{\pi }}\left[\ln(x/2)+\gamma \right]&{\mbox{if }}\alpha =0\\\\-{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{if }}\alpha >0\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c5777c6e6b7d6bc4064ded1cfb6dc31924c18c8)











![{\displaystyle \left({\frac {d}{xdx}}\right)^{m}\left[x^{\alpha }Z_{\alpha }(x)\right]=x^{\alpha -m}Z_{\alpha -m}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a5672cc4e621bb81e213314895df6ee45c8306b)
![{\displaystyle \left({\frac {d}{xdx}}\right)^{m}\left[{\frac {Z_{\alpha }(x)}{x^{\alpha }}}\right]=(-1)^{m}{\frac {Z_{\alpha +m}(x)}{x^{\alpha +m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c893320b4de90b0ae6f4341b45f589400aa5cd5)



