頻率分析
頻率分析在數學、物理學和信號處理中是一種分解函數、波形、或者信號的頻率組成,以獲取頻譜的方法。


在密碼學中,頻率分析是指研究字母或者字母組合在文本中出現的頻率。應用頻率分析可以破解古典密碼。
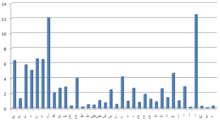
頻率分析基於如下原理:在任何一種書面語言中,不同的字母或字母組合出現的頻率各不相同。而且,對於以這種語言書寫的任意一段文本,都具有大致相同的特徵字母分布。比如,在英語中,字母E出現的頻率很高,而Z則出現得較少。類似地,ST、NG、TH,以及QU等雙字母組合出現的頻率非常高,NZ、QJ組合則極少。英語中出現頻率最高的12個字母可以簡記為「ETAOIN SHRDLU」。在現代標準漢語中,漢字「的」、「不」、「是」出現的頻率很高,而漢字「翊」、「謐」、「覷」則出現的較少,見常用國字標準字體表,後三個字屬於次常用字。
簡單替換密碼的頻率分析
[編輯]在一個簡單的替換密碼中,明文中的每一個字母都被另一個字母替換,而且明文中相同的字母在轉換為密文時總是被同一個字母所替換。比如,所有的e都會被替換成 X.一個含有大量X的密文消息會向密碼破譯者暗示X替換e.
一個例子
[編輯]現假設愛麗絲與鮑伯中的伊夫截獲了一段密碼(列於下方),它使用了一個簡單替換密碼進行加密:
LIVITCSWPIYVEWHEVSRIQMXLEYVEOIEWHRXEXIPFEMVEWHKVSTYLXZIXLIKIIXPIJVSZEYPERRGERIM WQLMGLMXQERIWGPSRIHMXQEREKIETXMJTPRGEVEKEITREWHEXXLEXXMZITWAWSQWXSWEXTVEPMRXRSJ GSTVRIEYVIEXCVMUIMWERGMIWXMJMGCSMWXSJOMIQXLIVIQIVIXQSVSTWHKPEGARCSXRWIEVSWIIBXV IZMXFSJXLIKEGAEWHEPSWYSWIWIEVXLISXLIVXLIRGEPIRQIVIIBGIIHMWYPFLEVHEWHYPSRRFQMXLE PPXLIECCIEVEWGISJKTVWMRLIHYSPHXLIQIMYLXSJXLIMWRIGXQEROIVFVIZEVAEKPIEWHXEAMWYEPP XLMWYRMWXSGSWRMHIVEXMSWMGSTPHLEVHPFKPEZINTCMXIVJSVLMRSCMWMSWVIRCIGXMWYMX
在這個例子中,大寫字母表示密文,小寫字母則表示明文(或猜測在這樣),而X~t用來代表一個關於:密文X 代表明文t的猜測。
伊夫可以使用頻率分析,以下面的消息來幫助解決密文大意:單字母中I最為常見;XL是最為常見的雙字母組;而XLI則為最為常見的三字母組,且密文中找不到D。根據英文的字母分布,e是最常見的單字母,th是最為常見的雙字母組,而the則為最為常見的三字母組。因些她猜測X~t、L~h及I~e。第二個密文中最常見的字母是E;t是英文中第二常見的字母,因此應該是E~t,但由於已假設X~t,所以伊夫暫且假設E~a。姑且讓這些假設進行解碼,獲得以下的(部分)已解密消息。
heVeTCSWPeYVaWHaVSReQMthaYVaOeaWHRtatePFaMVaWHKVSTYhtZetheKeetPeJVSZaYPaRRGaReM WQhMGhMtQaReWGPSReHMtQaRaKeaTtMJTPRGaVaKaeTRaWHatthattMZeTWAWSQWtSWatTVaPMRtRSJ GSTVReaYVeatCVMUeMWaRGMeWtMJMGCSMWtSJOMeQtheVeQeVetQSVSTWHKPaGARCStRWeaVSWeeBtV eZMtFSJtheKaGAaWHaPSWYSWeWeaVtheStheVtheRGaPeRQeVeeBGeeHMWYPFhaVHaWHYPSRRFQMtha PPtheaCCeaVaWGeSJKTVWMRheHYSPHtheQeMYhtSJtheMWReGtQaROeVFVeZaVAaKPeaWHtaAMWYaPP thMWYRMWtSGSWRMHeVatMSWMGSTPHhaVHPFKPaZeNTCMteVJSVhMRSCMWMSWVeRCeGtMWYMt
使用這些初始的猜測,伊夫發現了某些規律,來讓她可以確認其猜測,例如"that"。此外,其他規律則建議了進一步的猜測:"Rtate"可能是"state",即R~s。同樣,"atthattMZe"可以是"atthattime",寫出M~i及Z~m。而且,"heVe"可能是"here",給出V~r。再填入本來的密文,獲得:
hereTCSWPeYraWHarSseQithaYraOeaWHstatePFairaWHKrSTYhtmetheKeetPeJrSmaYPassGasei WQhiGhitQaseWGPSseHitQasaKeaTtiJTPsGaraKaeTsaWHatthattimeTWAWSQWtSWatTraPistsSJ GSTrseaYreatCriUeiWasGieWtiJiGCSiWtSJOieQthereQeretQSrSTWHKPaGAsCStsWearSWeeBtr emitFSJtheKaGAaWHaPSWYSWeWeartheStherthesGaPesQereeBGeeHiWYPFharHaWHYPSssFQitha PPtheaCCearaWGeSJKTrWisheHYSPHtheQeiYhtSJtheiWseGtQasOerFremarAaKPeaWHtaAiWYaPP thiWYsiWtSGSWsiHeratiSWiGSTPHharHPFKPameNTCiterJSrhisSCiWiSWresCeGtiWYit
反過來,這些猜測還建議一些例子(例如"remarA"可能是"remark",即A~k)。接著,相對簡單地就可推斷出其餘字母,最終產生明文:
hereuponlegrandarosewithagraveandstatelyairandbroughtmethebeetlefromaglasscasei nwhichitwasencloseditwasabeautifulscarabaeusandatthattimeunknowntonaturalistsof courseagreatprizeinascientificpointofviewthereweretworoundblackspotsnearoneextr emityofthebackandalongoneneartheotherthescaleswereexceedinglyhardandglossywitha lltheappearanceofburnishedgoldtheweightoftheinsectwasveryremarkableandtakingall thingsintoconsiderationicouldhardlyblamejupiterforhisopinionrespectingit
到了此時,伊夫便可以加上空格及標點符號:
Hereupon Legrand arose, with a grave and stately air, and brought me the beetle from a glass case in which it was enclosed. It was a beautiful scarabaeus, and, at that time, unknown to naturalists—of course a great prize in a scientific point of view. There were two round black spots near one extremity of the back, and a long one near the other. The scales were exceedingly hard and glossy, with all the appearance of burnished gold. The weight of the insect was very remarkable, and, taking all things into consideration, I could hardly blame Jupiter for his opinion respecting it.
其實這個例子是來自金甲蟲,正好伊夫的猜測全部正確。這並非總是如此,個別明文中的統計資料變化可能意味著最初的猜測並不正確。這樣可能就要做回溯法來更正錯誤或進一步推測。
明文中沒有表現出預期的字母頻率分佈也有可能。越短的消息越會表現出其更多的變化。明文本來就是經過人為扭曲的文本,例如整篇明文沒有了一些字母,通常會是最常見的「e」,這樣就稱為漏字文。
歷史和應用
[編輯]
第一個已知頻率分析(事實上,是任何一種密碼分析)的解釋是在9世紀時,阿拉伯博學家肯迪所著的《手稿上破譯加密消息》之上。[1] 它對於古蘭經的文本研究發現阿拉伯文有一個特別的字母頻率。其使用快速蔓延,類似的系統在文藝復興時期的歐洲國家十分流行。1474年,西科·西蒙內塔寫了一本手冊,上有關於破譯已加密的拉丁語和意大利語文本。[2]
密碼學家為加強簡單替換加密,使用了數項措施,包括:
- 使用「諧音替換法」 - 使用某幾個不太常用的字母替代最常見的字母(例如,在英語密文中,X和Y都可以代表明文E);
- 使用「多字母替換加密」 - 使用另一組文字作密錢來加密密鑰 - 參見多字母替換加密(萊昂·巴蒂斯塔·阿爾伯蒂可能是第一個這樣做的人);及
- 使用「表格式替換加密」,為每對字母進行加密,而非每個字母。例子為波雷費密碼。
所有這些抵禦頻率分析攻擊的嘗試都有一個缺點:它增加了加密和解密的難度,可能導致使用失誤。而最著名的的事件如下:最初英國外交部拒絕使用波雷費密碼,認為它太複雜。當惠斯登證明鄰近學校的四個男孩中,有三個可以在15分鐘內學會這種方法,外交部副秘書長的回應是:「這是有可能的,可惜你不能教曉那些高層人員。」
20世紀首50年,旋轉盤的使用興起(例如,恩尼格瑪密碼機),其基本上不會受到直接頻率分析攻擊。然而,其他種類的分析成功解譯了其中一些信息(其中最著名為Ultra計劃)。

頻率分析只需基本了解明文字母的統計,以及一些解決問題的能力,而且此方法可用人手解譯。在第二次世界大戰期間,英國與美國同時使用各大報紙上字謎和密碼比賽來招募解碼專家。軸心國中使用了某些很容易遭頻率分析破解的密碼(例如日本第二次世界大戰時的領事密碼)。機械替換加密或解密亦於第二次世界大戰之時開始使用。現時,頻率分析基本上全由電腦來完成,因此,現時替換式密碼很容易就被破解。
小說中的頻率分析
[編輯]阿瑟·柯南·道爾所寫的偵探小說《福爾摩斯‧歸來記》中《跳舞的人》篇中,福爾摩斯就在牆上看到五個跳舞人的畫,他從英語用語對答的常用性與英語使用頻率最高的字母E猜出了其中一次跳舞人畫所代表的字為Never,從而破解了字謎。
參考文獻
[編輯]引用
[編輯]- ^ Ibrahim A. Al-Kadi‧《密碼學的起源:阿拉伯國家的貢獻》,Cryptologia (頁面存檔備份,存於網際網路檔案館), 16(2) (1992年4月) pp. 97–126.
- ^ Kahn, David L. 密碼破譯者:加密的故事. 紐約: Scribner. 1996. ISBN 0-684-83130-9.
書籍
[編輯]- Helen Fouché Gaines, "Cryptanalysis", 1939, Dover. ISBN 978-0-486-20097-2
- Ibraham A. 「Al-Kindi: The origins of cryptology: The Arab contributions」, Cryptologia, 16(2) (April 1992) pp. 97–126.
- Abraham Sinkov, "Elementary Cryptanalysis : A Mathematical Approach", The Mathematical Association of America, 1966. ISBN 978-0-88385-622-2.
