數學中,Pin 群是一個二次型空間相伴的克利福德代數的一個子群。它有一個到正交群的 2 對 1 映射,就像 Spin 群映到特殊正交群一樣。
從 Pin 群到正交群的映射不是滿的也不是萬有覆疊空間,但對定二次型,兩者都正確。
確定形式的 Pin 群是到正交群的滿射,每個分支都是單連通的:它是正交群的二重覆疊。正定二次型  和它的負形式
和它的負形式  不是同構的,但是正交群是同構的
[註 1]。
不是同構的,但是正交群是同構的
[註 1]。
就標準形式而言, ,但是
,但是  。使用 Clifford 代數(這裡
。使用 Clifford 代數(這裡  )中通用的「±」號記法,我們可以寫成
)中通用的「±」號記法,我們可以寫成

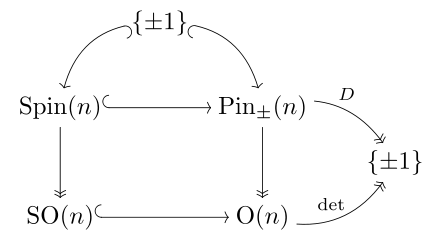
它們都是到  的滿射。
的滿射。
與之對比,我們有同構[註 2]  且他們都是特殊正交群 SO(n) 惟一的萬有覆疊。
且他們都是特殊正交群 SO(n) 惟一的萬有覆疊。
任何連通拓撲群在拓撲意義上有惟一的萬有覆疊空間,這個空間有惟一的群結構作為基本群的中心擴張。對一個不連通拓撲空間,含單位元的分支有一個惟一的萬有覆疊,然後在其他分支作為拓撲空間可取同一個覆疊(這是單位分支的主齊性空間),但是其它分支的群結構一般不是惟一的。
Pin 和 Spin 群是和正交群和特殊正交群關聯的獨特的拓撲空間,由 Clifford 代數中得出:存在其他類似的群,對于于其他分支的其他二重覆疊或者其他群結構,但是他們不叫做 Pin 或 Spin 群,研究得也少。
兩個 Pin 群對應於中心擴張

 (行列式為 1 的分支)上的群結構已經定義好了;其餘分支的群結構由中心確定,從而有一個
(行列式為 1 的分支)上的群結構已經定義好了;其餘分支的群結構由中心確定,從而有一個  分歧。
分歧。
兩個擴張由一個反射的原像的平方是  區分,這兩個 Pin 群即是這樣命名的。明確地說,一個反射在
區分,這兩個 Pin 群即是這樣命名的。明確地說,一個反射在  中的指數為 2,
中的指數為 2, ,所以反射的原像的平方(具有行列式 1)一定在
,所以反射的原像的平方(具有行列式 1)一定在  的核中,所以
的核中,所以  ,兩種選擇都確定了一個 Pin 群(因為所有反射共軛於聯通群
,兩種選擇都確定了一個 Pin 群(因為所有反射共軛於聯通群  的中一個元素,所有反射的平方一定具有相同值)。
的中一個元素,所有反射的平方一定具有相同值)。
具體地,在  中,
中, 的指數為 2,子群
的指數為 2,子群  的原像是
的原像是  :如果我們重複同一個反射,得到恆同。
:如果我們重複同一個反射,得到恆同。
在  中,
中, 的指數為 4:
如果重複同一個反射兩次,我們得到了一個「旋轉 2π」——
的指數為 4:
如果重複同一個反射兩次,我們得到了一個「旋轉 2π」—— 中的非平凡元可以理解為「旋轉 2π」(每一個軸得出相同的元素)。
中的非平凡元可以理解為「旋轉 2π」(每一個軸得出相同的元素)。
在 2 維, 與
與  的區別反映了一個正 2n 邊形的二面體群和循環群
的區別反映了一個正 2n 邊形的二面體群和循環群  的區別。
的區別。
在  中,一個正 2n 邊形的二面體群的原像,視為子群
中,一個正 2n 邊形的二面體群的原像,視為子群  ,是 2n 邊形的二面體群
,是 2n 邊形的二面體群  ;然而在
;然而在  中二面體群的原像是循環群
中二面體群的原像是循環群 
在 1維,Pin 群共軛於第一個二面體群和循環群:

Spin(p,q) 有八種不同的二重覆疊,對  ,這對應於用
,這對應於用  中心擴張(中心不是
中心擴張(中心不是  就是
就是  )。只有其中兩個稱為 Pin 群,他們可以將 Clifford 代數作為一個表示。他們分別稱為 Pin(p,q) 和 Pin(q,p)。
)。只有其中兩個稱為 Pin 群,他們可以將 Clifford 代數作為一個表示。他們分別稱為 Pin(p,q) 和 Pin(q,p)。
這個群的名稱在 邁克爾·阿蒂亞、拉烏爾·博特、A. Shapiro:
Clifford modules(Topology 3, suppl. 1 (1964), pp. 3-38, on page 3, line 17)一文中引入,他們說「這個笑話歸於 J-P. Serre」。這是「Spin」的逆構詞法:Pin 之於 Spin 就像 O(n) 之於 SO(n),從而從「Spin」中去掉「S」得到「Pin」。進一步,詞「Pin」的法語發音和一個粗痞話相同,這暗示了這個名稱的起源於(或被歸於)塞爾。[註 3]


































