使用者:Viztor/Binary search algorithm
| Viztor/Binary search algorithm | |
|---|---|
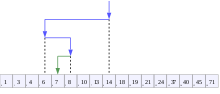 二叉搜索算法的演示,目標值為7 | |
| 概況 | |
| 複雜度 | |
| 相關變量的定義 |
二分搜索(也稱為折半搜索算法,對數搜索,或二進切分)是計算機科學中的一種在有序數組中搜索的搜索算法。二分搜索將目標值與數組的中間元素進行比較。[1][2] 如果不相等,則去掉目標值不可能存在的一半,並在另一半上進行搜索,再次將中間元素以目標值進行比較,重複這一過程,直到找到目標值。 如果搜索結束時剩下的一半為空,則目標不在數組中。 儘管想法簡單,但實現時,則需要特別注意其退出條件和中點的計算。
在最壞情況下,二分搜索以對數時間運行,進行 次比較操作(是數組中的元素數,是大 o 符號,是對數)。 二分搜索需要恆定的空間,這意味着該算法所占的空間對於任意數目元素數組都是相同的。[3] 二分搜索只能用於有序數組。除了小數組外,二分搜索比線性搜索更快。儘管專門用於快速搜索的數據結構可以更有效(如哈希表),但二分搜索更廣泛適用各種問題。
二進制搜索有許多不同分支。 比如:分級級聯加速多個數組中相同值的二進制搜索。 分數級聯有效地解決了計算幾何和許多其他字段中的一些搜索問題。 指數搜索將二進制搜索擴展到無界的列表。 二叉查找樹和 B-tree 數據結構是基於二進制搜索的。
算法
[編輯]對排序數組進行二進制搜索。 二進制搜索首先將數組的中間元素與目標值進行比較。 如果目標值與中間元素相匹配,則返回其在數組中的位置。 如果目標值小於中間元素,則搜索繼續在數組的下半部分。 如果目標值大於中間元素,則搜索繼續在數組的上半部分。 通過這樣做,算法消除了目標值不能在每個迭代中隱藏的一半。
程序
[編輯]Given an array of elements with values or records sorted such that , and target value , the following subroutine uses binary search to find the index of in .[4]
- Set to and to .
- If , the search terminates as unsuccessful.
- Set (the position of the middle element) to the floor of , which is the greatest integer less than or equal to .
- If , set to and go to step 2.
- If , set to and go to step 2.
- Now , the search is done; return .
This iterative procedure keeps track of the search boundaries with the two variables and . The procedure may be expressed in pseudocode as follows, where the variable names and types remain the same as above, floor is the floor function, and unsuccessful refers to a specific value that conveys the failure of the search.[4]
[[Category:二]]
[[Category:搜尋演算法]]
[[Category:Webarchive模板wayback链接]]
[[Category:CS1匈牙利文来源 (hu)]]
[[Category:Pages with unreviewed translations]]
- ^ 空引用 (幫助)
- ^ 埃里克·韋斯坦因. Binary search. MathWorld.
- ^ Flores, Ivan; Madpis, George. Average binary search length for dense ordered lists. Communications of the ACM. 1 September 1971, 14 (9): 602–603 [29 June 2018]. Bibcode:1985CACM...28...22S. ISSN 0001-0782. doi:10.1145/362663.362752.
- ^ 4.0 4.1 Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "Algorithm B".





















