三相交通理論

三相交通理論，是玻里斯·柯納在1996至2002年間提出的一種交通流理論^[1]^[2]^[3] 。它着重研究如何解釋高速公路上交通擁堵轉捩的物理原理以及擁堵交通流的性質。不同於經典的基於基本圖的交通流理論將交通流劃分為自由流和擁堵流兩相的做法，柯納將擁堵流進一步劃分為同步流和寬運動堵塞兩相，從而得到以下的三相：

自由流（Free flow, F）
同步流（Synchronized flow, S）
寬運動堵塞（Wide moving jam, J）

這裏「相」定義為某種時空狀態。

自由流（F）

實測數據顯示，在自由流中交通流量 q （車輛數/時間單位）和車輛密度 k （車輛數/長度單位）存在正相關性。這一關係的上邊界，也即最大流量，在臨界密度 $k_{crit}$ 處取得。參見圖1.

擁堵交通流

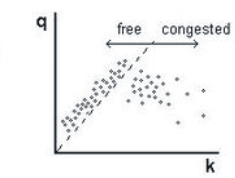
在擁堵交通流中，車輛速度比在自由流中能達到的最低車速 $v_{free}^{min}$ 還要低。通常 $v_{free}^{min}$ 可以通過最大流量和臨界密度求得 $v_{free}^{min}={\frac {q_{max}}{k_{crit}}}$ ，在 $k-q$ 圖中， $v_{free}^{min}$ 是從原點出發，通過( $q_{max}$ , $k_{crit})$ 這條直線的斜率(圖2虛線所示)。該線將流量－密度圖上的實測數據點分為兩個部分：位於左側的自由流數據點和位於右側的擁堵流數據點。

擁堵流中寬運動堵塞相 J 和同步流相 S 的定義

柯納根據常見的實際交通流時空特徵對擁堵流中寬運動堵塞相 J 和同步流相 S進行了如下定義：

寬運動堵塞相 J 的定義：一個寬運動堵塞通過一個高速公路瓶頸時，其下游分界面（downstream front）向上游的平均傳播速度 $v_{g}$ 保持不變。車輛加速通過堵塞下游分界面駛離堵塞，進入自由流或同步流狀態。這就是寬運動阻塞的本質特徵。

同步流相 S 的定義：在同步流下游分界面，車輛加速進入自由流狀態。同步流的下游分界面不再呈現寬運動堵塞下游分界面的特性，其傳播速度並不是一個常數。且通常情況下同步流的下游分界面固定在瓶頸處不動。

通過車輛平均速度的測量，我們可以這樣解釋寬運動堵塞相 J 和同步流相 S 的定義。圖3(a)中顯示了低速擁堵流有着兩種時空特徵。一種是擁堵流下游分界面的向上游傳播的速度幾乎為常數，且可以通過瓶頸不受影響；根據上述定義，這種交通流為寬運動阻塞相。另一種是擁堵流下游分界面固定在瓶頸處；根據上述定義，這種交通流為同步流相。

F → S的相變：交通擁堵轉捩

在實測中，擁擠交通往往出現在道路瓶頸處，如入匝道，出匝道，道路工事等。這種自由流至擁擠交通的轉變被稱為交通擁堵轉捩。在柯納的三相交通理論中這種交通擁堵轉捩被解釋為一個F → S相變。這一解釋由已有觀測支持，因為在實測交通數據中，當瓶頸處發生交通擁堵轉捩後，擁擠交通的下游分界面固定在瓶頸處。因此，交通擁堵轉捩後出現的擁擠交通符合「同步流」交通相的定義。

柯納指出，實測數據顯示，同步流可自發的在自由流中出現(自發F → S相變)或者由外部擾動誘導出現(誘導的F → S相變)。自發的F → S相變意味着在交通擁堵轉捩前，瓶頸上下游皆出於自由流狀態，即自發的F → S相變是由於瓶頸附近交通流內在擾動的發展演化而成。與之不同，誘導的F → S相變是由於遠離瓶頸處的外在擾動發展演化而成。一般來說，這種相變與向上游傳播的同步流或寬運動堵塞相關。圖3給出了一個瓶頸附近誘導發生的交通擁堵轉捩，而形成同步流的實例：同步流是由於寬運動堵塞向上游傳播而形成。

柯納解釋F → S相變是由於車輛加速超越前方慢車和車輛減速到前方慢車速度(速度適配,speed adaptation)這兩種因素的時空競爭。超車造就自由流，速度適配導致同步流。當車輛無法超車時，將會發生速度適配。柯納指出超車概率是車輛密度的間斷函數(圖4)：在一個給定的車輛密度，自由流中的超車概率遠大於同步流中的超車概率。

圖4 柯納的三相交通理論中，使用Z型非線性超車概率的間斷函數解釋交通擁堵轉捩。虛線表示臨界超車概率和交通密度之間的函數關係。

道路通行能力的無窮多值性

自發的交通擁堵轉捩（例如一個自發的自由流到同步流的相變）可能在流量範圍很寬的自由流中發生。根據實測數據，柯納認為，由於自發或者瓶頸誘導的交通擁堵轉捩的隨機性，道路通行能力有無窮多個值。其大小在最低通行能力 $q_{th}$ 到自由流所代表的最大通行能力 $q_{max}$ 之間，參見圖5。

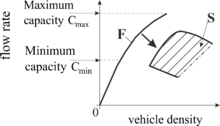
在自由流的流量接近最大通行能力 $q_{max}$ 時，只有自由流中的小擾動才能導致在瓶頸處出現自發的自由流向同步流的相變。另一方面，當流量接近最小通行能力 $q_{min}$ 時，只有大的擾動才能導致在瓶頸處出現自發的自由流向同步流的相變。在自由流中出現大擾動的概率要遠小於出現小擾動的概率。因此，在瓶頸處的交通流流量越大，出現自發的自由流到同步流相變的概率越大。如果交通流流量小於最小通行能力 $q_{th}$ ，則不會在瓶頸處發生交通擁堵轉捩，也即自由流向同步流的相變。

這種道路通行能力的無窮多值性可以通過自由流在流量 $q$ 情況下的亞穩定性來解釋。自由流的亞穩定性是指在小擾動下，自由流可以保持穩定（繼續為自由流）；但在大的擾動下，可能失穩，發生自由流向同步流的相變。

柯納三相交通理論假定的道路通行能力的無窮多值性和用於交通管理和控制的經典交通理論方法不同；後者假定任何時候只可能存在一個特定的道路通行能力。

寬運動阻塞(J)

一個寬運動阻塞之所以被形容為「寬」，是因為沿着交通流的方向，阻塞區域寬度顯著超過了阻塞分界面的寬度。在寬運動阻塞中，車輛速度要大大低於自由流中的車輛速度。在寬運動阻塞的下游分界面處，車輛有可能加速到自由流速度。而在寬運動阻塞的上游分界面處，來自自由流或同步流的車輛將減速。根據定義，寬運動阻塞在傳播通過其它相或瓶頸時將保持其下游分界面傳播的平均速度 $v_{g}$ 。在寬運動阻塞中，交通流量將嚴重下降。

柯納的實測結果表明，寬運動阻塞的某些特徵和交通流流量以及瓶頸屬性（例如何時何處產生阻塞）無關。但是這些特徵和天氣狀況，道路狀況，車輛技術，長車比例等有關。寬運動阻塞的下游分界面向上游傳播的速度 $v_{g}$ 和流出下游分界面的流量 $q_{out}$ （出流為自由流時）是兩個特徵參數，參見圖6。這表明在類似的條件下，幾個寬運動阻塞有着類似的特徵。基於此，這兩個參數較容易預測。在流量－密度圖中，下游分界面的移動可以用一條叫做堵塞J線(Line Jam)的直線表示，其斜率為 $v_{g}$ ，該直線和橫軸的交點在最大密度處。

柯納強調，最小通行能力 $q_{th}$ 和流出寬運動阻塞的流量 $q_{out}$ 描述了兩種本質不同自由流。最小通行能力 $q_{th}$ 描述的是瓶頸處自由流到同步流的相變，即交通擁堵轉捩。而流出寬運動阻塞的流量 $q_{out}$ 描述的是交通阻塞存在的條件，也就阻塞相。在自由流向同步流相變處，根據交通參數（比如天氣，長車比例和瓶頸特徵等）的不同， $q_{th}$ 可能比 $q_{out}$ 要大（如圖6所示），也可能要小。而靠近運動阻塞下游分界面的窄運動阻塞的增長可能會受到抑制。

同步流(S)

和寬運動阻塞不同，在同步流中，交通流流量和車輛速度可能發生顯著的變化。同步流的下游分界面通常保持在瓶頸或者道路某處。相對於自由流，處於同步流的車輛速度將顯著下降，但交通流量可以大致維持在與自由流相當的水平。

由於同步流沒有寬運動阻塞所特有的性質，柯納的三相交通理論假定均勻同步流將在流量－密度平面上佔據一個二維區域（參見圖6的陰影區域）。

同步流到寬運動阻塞的相變

寬運動阻塞不會在自由流中自發產生，但能在同步流中自發產生。這種相變被稱為同步流到寬運動阻塞（S→J）的相變。

因此，從自由流產生寬運動阻塞可以被視為一個自由流到同步流再到寬運動阻塞的逐級相變過程(F → S → J)。首先，自由流中的某個區域將轉變為同步流。按照上面的解釋，這一區域通常位於瓶頸附近。在同步流中，將發生自擠壓過程(self-compression)使得車輛密度升高而車輛速度下降。這種自擠壓過程被稱為擠壓效應(pinch effect)。在同步流的擠壓區域（pinch region），窄運動阻塞將出現。隨着這些窄運動阻塞的增長，寬運動阻塞將形成。柯納指出隨着寬運動阻塞發生的頻率增加，同步流的密度將增加。寬運動阻塞將向上游傳播，甚至跨過同步流區域或瓶頸。

根據柯納的三相交通理論，我們可以對同步流到寬運動阻塞進一步解釋。堵塞J線將同步流的均勻狀態分為兩個部分（圖6），其中位於J線以上的為亞穩態，也即有小擾動時，同步流維持穩定，而發生大擾動時，發生同步流到阻塞流的相變；而位於J線以下的為穩態，不會發生同步流到阻塞流的相變。

源自S 和J的交通形態

由於F → S 和 S → J 相變，可觀測到非常複雜的擁擠形態。下游分界面固定，上游分界面不持續傳播的同步流擁擠形態稱為局部同步流形態 (localized synchronized flow pattern, LSP)。

同步流形態的上游分界面經常是向上游傳播的，如果僅僅上游分界面向上游傳播，對應的同步流形態稱為擴張的同步流形態(widening synchronized flow pattern, WSP)。WSP的下游分界面固定在瓶頸處，其寬度不斷增加。

同步流形態的上下游分界面都可能向上游傳播，下游分界面不再固定在瓶頸處。這種形態稱為移動的同步流形態(Moving Synchronized Flow Pattern, MSP)。

當WSP或者MSP到達上游瓶頸時，同步流形態和寬運動堵塞的區別變得十分明顯：即所謂的捕捉效應(catch effect)。同步流形態將被捕捉固定到瓶頸處，因此產生一個新的擁擠形態。寬運動堵塞不會被捕捉固定，它繼續向上游傳播。和寬運動堵塞不同，同步流形態，即使是MSP也沒有特徵傳播速度參數，不同MSP的下游分界面傳播速度可能顯著不同。這些同步流形態和寬運動堵塞的特性都是S和J的相定義的結果。

一個典型的擁擠形態可能包括S和J兩個擁擠相。這樣的形態稱為普遍形態（General Pattern，GP)。

在很多高速公路上，結構瓶頸彼此相距很近。同步流區跨越兩個或更多瓶頸的擁擠形態稱為擴展形態(expanded pattern, EP)。一個EP可以只包含同步流，稱為擴展的同步流形態(expanded synchronized flow pattern, ESP)，但一般情況下同步流中會出現寬運動堵塞。這種情況下EP稱為擴展的普遍形態(expanded general pattern， EGP), 見圖7。

三相交通理論在交通工程中的應用

柯納三相交通理論的一個應用是Automatische StauDynamikAnalyse (寬運動阻塞的自動跟蹤，ASDA)方法和 Forecasting Of Traffic Objects (交通對象預測,FOTO)系統。ASDA/FOTO作為一個軟件工具能快速處理大量交通數據，提高高速公路網絡的效率（參見在三個國家應用的情況，圖8）。ASDA/FOTO在使用交通實測數據的在線交通管理系統中得到了應用。其中同步流和堵塞的辨識，跟蹤和預測均根據柯納的三相交通理論來實現。

三相交通流理論的進一步應用還包括交通仿真模型，匝道控制（ANCONA）算法，集成交通控制，交通輔助和交通狀態檢測。這些都在柯納的專著中詳加論述。

出版專著

參考文獻

註釋(Notes)

^ Boris S. Kerner, "Experimental Features of Self-Organization in Traffic Flow", Physical Review Letters, 81, 3797-3400 (1998). [2010-04-14]. （原始內容存檔於2011-09-27）.
^ Boris S. Kerner, "The physics of traffic", Physics World Magazine 12, 25-30 (August 1999). [2010-04-14]. （原始內容存檔於2011-07-21）.
^ Boris S. Kerner, "Congested Traffic Flow: Observations and Theory", Transportation Research Record, Vol. 1678, pp. 160-167 (1999). [2010-04-14]. （原始內容存檔於2012-12-09）.

參見

交通流基本圖（英語：Fundamental diagram of traffic flow）
交通流
交通波（英語：Traffic wave）
交通堵塞

[PhysRevLetters1998-1] Boris S. Kerner, "Experimental Features of Self-Organization in Traffic Flow", Physical Review Letters, 81, 3797-3400 (1998). [2010-04-14]. （原始內容存檔於2011-09-27）.

[PhysicsWorld1999-2] Boris S. Kerner, "The physics of traffic", Physics World Magazine 12, 25-30 (August 1999). [2010-04-14]. （原始內容存檔於2011-07-21）.

[TRB1999-3] Boris S. Kerner, "Congested Traffic Flow: Observations and Theory", Transportation Research Record, Vol. 1678, pp. 160-167 (1999). [2010-04-14]. （原始內容存檔於2012-12-09）.

[1]

[2]

[3]