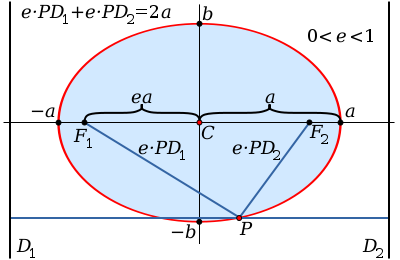
 橢圓和它的某些數學性質
橢圓和它的某些數學性質
在數學中,橢圓是平面上到兩個相異固定點的距離之和為常數的點之軌跡。
根據該定義,可以用手繪橢圓:先準備一條線,將這條線的兩端各綁在固定的點上(這兩個點就當作是橢圓的兩個焦點,且距離小於線長);取一支筆,用筆尖將線繃緊,這時候兩個點和筆就形成一個三角形(的兩邊);然後左右移動筆尖拉住線開始作圖,持續地使線繃緊,最後就可以完成一個橢圓圖形。
由於兩個固定點之間的距離也是一定的,所以可以省去綁在點上這一步驟而改將線綁成環狀,然後以筆尖和這兩個焦點將線繃直即可。下同。
 一個平面切截一個圓錐面得到的橢圓。
一個平面切截一個圓錐面得到的橢圓。
橢圓是一種圓錐曲線:如果一個平面切截一個圓錐面,且不與它的底面相交,也不與它的底面平行,則圓錐和平面交截線是個橢圓。
在代數上說,橢圓是在笛卡爾平面上如下形式的方程所定義的曲線

使得  ,這裏的係數都是實數,並存在定義在橢圓上的點對 (x, y) 的多於一個的解。
,這裏的係數都是實數,並存在定義在橢圓上的點對 (x, y) 的多於一個的解。
穿過兩焦點並終止於橢圓上的線段AB叫做長軸。長軸是通過連接橢圓上的兩個點所能獲得的最長線段。穿過中心(兩焦點的連線的中點)垂直於長軸並且終止於橢圓的線段CD叫做短軸。半長軸(圖中指示為 a)是長軸的一半:從中心通過一個焦點到橢圓的邊緣的線段。半短軸(圖中指示為 b)是短軸的一半。
如果兩個焦點重合,則這個橢圓是圓;換句話說,圓是離心率為零的橢圓。
中心位於原點的橢圓  可以被看作單位圓在關聯於對稱矩陣
可以被看作單位圓在關聯於對稱矩陣  的線性映射下的圖像,這裏的 D 是帶有
的線性映射下的圖像,這裏的 D 是帶有  的特徵值的對角矩陣,二者沿着主對角線都是正實數的,而 P 是擁有
的特徵值的對角矩陣,二者沿着主對角線都是正實數的,而 P 是擁有  的特徵向量作為縱列的實數的酉矩陣。橢圓的長短軸分別沿着
的特徵向量作為縱列的實數的酉矩陣。橢圓的長短軸分別沿着  的兩個特徵向量的方向,而兩個與之對應的特徵值分別是半長軸和半短軸的長度的平方的倒數。
的兩個特徵向量的方向,而兩個與之對應的特徵值分別是半長軸和半短軸的長度的平方的倒數。
橢圓可以通過對一個圓的所有點的 x 坐標乘以一個常數而不改變 y 坐標來生成。
 形狀母數:
形狀母數:- C:中心
- F1:焦點一;
- F2:焦點二;
- a:半長軸;
- b:半短軸;
- c:半焦距;
- p:半正焦弦(通常標示作
 )。
)。
橢圓的形狀可以用叫做橢圓的離心率的一個數來表達,習慣上指示為  。離心率是小於 1 大於等於 0 的實數。離心率 0 表示着兩個焦點重合而這個橢圓是圓。
。離心率是小於 1 大於等於 0 的實數。離心率 0 表示着兩個焦點重合而這個橢圓是圓。
對於有半長軸 a 和半短軸 b 的橢圓,離心率是

離心率越大,a 與 b 的比率就越大,因此橢圓被更加拉長。
半焦距c 等於從中心到任一焦點的距離,

則

半焦距 c 也叫做橢圓的線性離心率。在兩個焦點間的距離是 2c = 2aε。
 在正規位置上的橢圓的參數方程。參數 t 是藍線對於 X-軸的角度。
在正規位置上的橢圓的參數方程。參數 t 是藍線對於 X-軸的角度。
中心位於點  的主軸平行於 x 軸的橢圓由如下方程指定
的主軸平行於 x 軸的橢圓由如下方程指定

這個橢圓可以參數化表達為


這裏的  可以限制於區間
可以限制於區間  。
。
如果  且
且  (就是說,如果中心是原點(0,0)),則
(就是說,如果中心是原點(0,0)),則


這個參數方程揭示了兩個方向相互垂直的簡諧運動(表現為具有周期性的簡諧波)合成了閉合的橢圓形周期性運動(表現為軌跡是橢圓)。
| 橢圓方程
|

|

|
| 圖像
|
|
|
| 範圍
|

|

|
用極坐標可表達為

這裏的  是橢圓的離心率;
是橢圓的離心率; 是
是  與
與  的夾角
的夾角
 橢圓的極坐標,原點在 F1
橢圓的極坐標,原點在 F1
有一個焦點在原點的橢圓的極坐標方程是

這裏的  是
是  與
與  的夾角
的夾角
橢圓的半正焦弦(通常指示為  ),是從橢圓的一個焦點到橢圓自身,沿着垂直主軸的直線測量的距離。它有關於
),是從橢圓的一個焦點到橢圓自身,沿着垂直主軸的直線測量的距離。它有關於  和
和  (橢圓的半軸),通過公式
(橢圓的半軸),通過公式  或者如果使用離心率的話
或者如果使用離心率的話  。
。
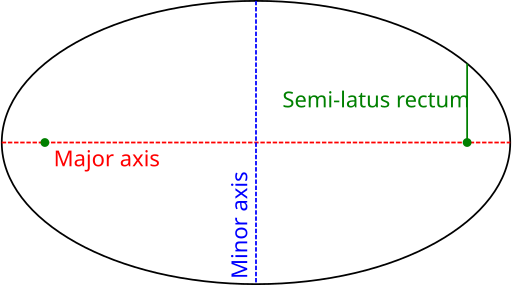 橢圓,使用半正焦弦展示
橢圓,使用半正焦弦展示
在極坐標中,一個焦點在原點而另一個焦點在負 x 軸上的橢圓給出自方程

橢圓可以被看作是圓的投影:在與水平面有角度 φ 的平面上的圓垂直投影到水平面上給出離心率 sin φ 的橢圓,假定 φ 不是 90°。
 橢圓(用紅色繪制)可以表達為內旋輪線在 R=2r 時的特殊情況。
橢圓(用紅色繪制)可以表達為內旋輪線在 R=2r 時的特殊情況。
橢圓所包圍的面積是  ,這裏的
,這裏的  ,和
,和 ,
是半長軸和半短軸。在圓的情況下
,
是半長軸和半短軸。在圓的情況下 ,表達式簡化為
,表達式簡化為  。
。
橢圓的周長是  ,這裏的函數
,這裏的函數 是第二類完全橢圓積分。
是第二類完全橢圓積分。
周長為: 或者
或者
精確的無窮級數為:
![{\displaystyle C=2\pi a\left[{1-\left({1 \over 2}\right)^{2}{\frac {c^{2}}{a^{2}}}-\left({1\cdot 3 \over 2\cdot 4}\right)^{2}{c^{4} \over {3a^{4}}}-\left({1\cdot 3\cdot 5 \over 2\cdot 4\cdot 6}\right)^{2}{c^{6} \over {5a^{6}}}-\dots }\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dfada5024276d3f82d18f849a5b95fb332eaacb)
或:
![{\displaystyle C=-2\pi a\sum _{n=0}^{\infty }{\left\lbrace \left[\prod _{m=1}^{n}\left({2m-1 \over 2m}\right)\right]^{2}{c^{2n} \over {{a^{2n}}\left(2n-1\right)}}\right\rbrace }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a57534cbe1f8f5c5b5fb48f3be75f7b37ec9f5ae)
拉馬努金給出一較為接近的式子:
![{\displaystyle C\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd246503ae5e29912d4149f118c5d7145d637085)
它還可以寫為:
![{\displaystyle C\approx 3a\pi \left[1+{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]-a\pi {\sqrt {\left[3+{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]\left[1+3{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]}}\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ad92a27ab7667d10fcdd89db63ed66ba331cc1)
還有一條近似很高的公式:
![{\displaystyle C\approx \pi (a+b)\left[1+{\frac {3\left({\frac {a-b}{a+b}}\right)^{2}}{10+{\sqrt {4-3\left({\frac {a-b}{a+b}}\right)^{2}}}}}\right]\left[1+\left({\frac {22}{7\pi }}-1\right)\left({\frac {a-b}{a}}\right)^{33}{\sqrt[{1000}]{\left({\frac {a-b}{a}}\right)^{697}}}\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62aa6152db65a0903657774d16c0477e7ea273d6)
- 如果在一個平面內一個動點到兩個定點的距離的和等於定長,那麼這個動點的軌跡叫做橢圓。
假設(注意所有假設只是為了導出橢圓方程時比較簡便)動點為 ,兩個定點為
,兩個定點為 和
和 ,則根據定義,動點
,則根據定義,動點 的軌跡方程滿足(定義式):
的軌跡方程滿足(定義式):
 ,其中
,其中 為定長。
為定長。
用兩點的距離公式可得: ,
, ,代入定義式中,得:
,代入定義式中,得:
 ①
①
上式左方分子湊出平方差,並化簡,得:
![{\displaystyle {\frac {\left(x+c\right)^{2}+y^{2}-\left[\left(x-c\right)^{2}+y^{2}\right]}{{\sqrt {\left(x+c\right)^{2}+y^{2}}}-{\sqrt {\left(x-c\right)^{2}+y^{2}}}}}=2a\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc56759682756dfdc31a8718c98b6a251963920d)
分子大部分相消,分母移項即得
 ②
②
①、②式相加並平方,整理得

當 時,並設
時,並設 ,則上式可以進一步化簡:
,則上式可以進一步化簡:

因為 ,將上式兩邊同除以
,將上式兩邊同除以 ,可得:
,可得:

則該方程即動點 的軌跡方程,即橢圓的方程。這個形式也是橢圓的標準方程。
的軌跡方程,即橢圓的方程。這個形式也是橢圓的標準方程。
- 橢圓的圖像如果在直角坐標系中表示,那麼上述定義中兩個定點被定義在了x軸。若將兩個定點改在y軸,可以用相同方法求出另一個橢圓的標準方程:

- 在方程中,所設的
 稱為長軸長,
稱為長軸長, 稱為短軸長,而所設的定點稱為焦點,那麼
稱為短軸長,而所設的定點稱為焦點,那麼 稱為焦距。在假設的過程中,假設了
稱為焦距。在假設的過程中,假設了 ,如果不這樣假設,會發現得不到橢圓。當
,如果不這樣假設,會發現得不到橢圓。當 時,這個動點的軌跡是一個線段;當
時,這個動點的軌跡是一個線段;當 時,根本得不到實際存在的軌跡,而這時,其軌跡稱為虛橢圓。另外還要注意,在假設中,還有一處:
時,根本得不到實際存在的軌跡,而這時,其軌跡稱為虛橢圓。另外還要注意,在假設中,還有一處: 。
。
- 通常認為圓是橢圓的一種特殊情況。
對於平面上任意橢圓  ,總可以將之轉化為
,總可以將之轉化為

的形式。具體步驟為,將後式的各乘積乘方項展開,根據與前式對應項係數相等的法則便可求得u,v,D',E',F'的值( ,
,  ,
,  )。其中,
)。其中, 便是該橢圓的中心(F'=0)。
便是該橢圓的中心(F'=0)。
若將


代入式中便可得到平移前的橢圓。
若 ,則表示橢圓的長短軸與坐標系的坐標軸並不平行或垂直,即發生了旋轉。設旋轉的角度為
,則表示橢圓的長短軸與坐標系的坐標軸並不平行或垂直,即發生了旋轉。設旋轉的角度為 ,則有
,則有

當 ,則說明
,則說明 。
。
若將


代入式中便可得到旋轉前的橢圓。

![{\displaystyle {\begin{cases}{\cfrac {{\rm {d}}x}{\rm {{d}t}}}={\cfrac {\left[b^{2}\sin 2t-2b^{2}\sin t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\right]\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right)-ab\left(a^{2}-b^{2}\right)\sin 2t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\sin t}{2\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right){\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}}}-a\sin t\!\,\\\\{\cfrac {{\rm {d}}y}{\rm {{d}t}}}={\cfrac {\left[b^{3}\sin 2t-2ab^{2}\sin t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\right]\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right)-ab^{2}\left(a^{2}-b^{2}\right)\sin 2t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\sin t}{2a\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right){\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}}}+b\cos t\!\,\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fb25c21dda4b86817dbaf019bd92ed03bb4bd94)
有了橢圓漸開線的導數,可以計算它的長度,其中 是第二類完全橢圓積分。
是第二類完全橢圓積分。
























































![{\displaystyle C=2\pi a\left[{1-\left({1 \over 2}\right)^{2}{\frac {c^{2}}{a^{2}}}-\left({1\cdot 3 \over 2\cdot 4}\right)^{2}{c^{4} \over {3a^{4}}}-\left({1\cdot 3\cdot 5 \over 2\cdot 4\cdot 6}\right)^{2}{c^{6} \over {5a^{6}}}-\dots }\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dfada5024276d3f82d18f849a5b95fb332eaacb)
![{\displaystyle C=-2\pi a\sum _{n=0}^{\infty }{\left\lbrace \left[\prod _{m=1}^{n}\left({2m-1 \over 2m}\right)\right]^{2}{c^{2n} \over {{a^{2n}}\left(2n-1\right)}}\right\rbrace }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a57534cbe1f8f5c5b5fb48f3be75f7b37ec9f5ae)
![{\displaystyle C\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd246503ae5e29912d4149f118c5d7145d637085)
![{\displaystyle C\approx 3a\pi \left[1+{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]-a\pi {\sqrt {\left[3+{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]\left[1+3{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]}}\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ad92a27ab7667d10fcdd89db63ed66ba331cc1)
![{\displaystyle C\approx \pi (a+b)\left[1+{\frac {3\left({\frac {a-b}{a+b}}\right)^{2}}{10+{\sqrt {4-3\left({\frac {a-b}{a+b}}\right)^{2}}}}}\right]\left[1+\left({\frac {22}{7\pi }}-1\right)\left({\frac {a-b}{a}}\right)^{33}{\sqrt[{1000}]{\left({\frac {a-b}{a}}\right)^{697}}}\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62aa6152db65a0903657774d16c0477e7ea273d6)









![{\displaystyle {\frac {\left(x+c\right)^{2}+y^{2}-\left[\left(x-c\right)^{2}+y^{2}\right]}{{\sqrt {\left(x+c\right)^{2}+y^{2}}}-{\sqrt {\left(x-c\right)^{2}+y^{2}}}}}=2a\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc56759682756dfdc31a8718c98b6a251963920d)





























![{\displaystyle {\begin{cases}{\cfrac {{\rm {d}}x}{\rm {{d}t}}}={\cfrac {\left[b^{2}\sin 2t-2b^{2}\sin t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\right]\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right)-ab\left(a^{2}-b^{2}\right)\sin 2t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\sin t}{2\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right){\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}}}-a\sin t\!\,\\\\{\cfrac {{\rm {d}}y}{\rm {{d}t}}}={\cfrac {\left[b^{3}\sin 2t-2ab^{2}\sin t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\right]\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right)-ab^{2}\left(a^{2}-b^{2}\right)\sin 2t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\sin t}{2a\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right){\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}}}+b\cos t\!\,\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fb25c21dda4b86817dbaf019bd92ed03bb4bd94)
