短時距傅利葉變換

短時距傅利葉變換（Short-time Fourier Transform, STFT）是傅利葉變換的一種變形，也稱作加窗傅利葉轉換（Windowed Fourier transform）或Time-dependent Fourier transform，用於決定隨時間變化的訊號局部部分的正弦頻率和相位。實際上，計算短時距傅利葉變換的過程是將長時間訊號分成數個較短的等長訊號，然後再分別計算每個較短段的傅利葉轉換。通常拿來描繪頻域與時域上的變化，為時頻分析中其中一個重要的工具。

與傅利葉轉換在概念上的區別

將訊號做傅利葉變換後得到的結果，並不能給予關於訊號頻率隨時間改變的任何資訊。以下的例子作為說明：

$x(t)={\begin{cases}\cos(440\pi t);&t<0.5\\\cos(660\pi t);&0.5\leq t<1\\\cos(524\pi t);&t\geq 1\end{cases}}$

傅利葉變換後的頻譜和短時距傅利葉轉換後的結果如下：

傅利葉轉換後, 橫軸為頻率(赫茲)

短時距傅利葉轉換, 橫軸為時間(秒)，縱軸為頻率(赫茲)

由上圖可發現，傅利葉轉換只提供了有哪些頻率成份的資訊，卻沒有提供時間資訊；而短時傅利葉轉換則清楚的提供這兩種資訊。這種時頻分析的方法有利於頻率會隨着時間改變的訊號，如音樂訊號和語音訊號等分析。

定義

連續短時傅利葉轉換

簡單來說，在連續時間的例子，一個函數可以先乘上僅在一段時間不為零的窗函數再進行一維的傅利葉變換。再將這個窗函數沿着時間軸挪移，所得到一系列的傅利葉變換結果排開則成為二維表象。數學上，這樣的操作可寫為：

$X(t,f)=\int _{-\infty }^{\infty }w(t-\tau )x(\tau )e^{-j2\pi f\tau }\,d\tau$

另外也可用角頻率來表示：

$X(t,\omega )=\int _{-\infty }^{\infty }w(t-\tau )x(\tau )e^{-j\omega \tau }\,d\tau$

其中$w(t)$是窗函數，窗函數種類有很多種，會在稍後再做仔細討論。$x(t)$是待變換的訊號。$X(t,\omega )$是$w(t-\tau )x(\tau )$的傅利葉變換。 隨着$t$的改變，窗函數在時間軸上會有位移。經$w(t-\tau )x(\tau )$後，訊號只留下了窗函數截取的部分做最後的傅利葉轉換，所得到的結果為一複數函數，代表着訊號隨時間與頻率變化的大小與相位。

離散短時傅利葉轉換

在離散時間的例子，資料會被切割成數個大量的幀，而每組幀通常會互相重疊，避免因切割方式造成邊界的誤差。而每組幀在各自進行傅利葉轉換後所得的複數結果會再進行相加，可得到每個點時間與頻率變化的大小與相位。數學上，這樣的操作可寫為：

$\mathbf {STFT} \{x[n]\}(m,\omega )\equiv X(m,\omega )=\sum _{n=-\infty }^{\infty }x[n]w[n-m]e^{-j\omega n}$

相同地，其中$w[n]$是窗函數，$x[n]$是待變換的訊號。在這個例子裏，m是離散的且ω是連續的，但大部分實際的應用當中，短時距傅利葉轉換在電腦中都是以快速傅利葉轉換進行計算(見實現方法的快速傅利葉變換)，而此時這兩個參數都是離散且被量化的。

Sliding 離散傅利葉轉換

當只想要得知特定少數的ω，或是短時距傅利葉轉換每次窗函數移動m的值，則短時距傅利葉轉換可以利用sliding DFT演算法更有效地計算出來。

反短時距傅利葉轉換

短時距傅利葉轉換是可逆的，也就是說原本的訊號可以藉由反短時距傅利葉轉換將短時距傅利葉轉換後的訊號還原。

其中最廣為接受的反短時距傅利葉轉換方法是重疊-相加之摺積法，此方法也促成了更多樣的訊號處理方法。

反短時距傅利葉轉換，其數學類似傅利葉轉換，但須消除窗函數的作用，首先必須先將窗函數的總面積規模化使得

$\int _{-\infty }^{\infty }w(\tau )\,d\tau =1.$

而從上也可輕易地得出

$\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =1\quad \forall \ t$

和

$x(t)=x(t)\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau .$

連續傅利葉轉換公式如下：

$X(\omega )=\int _{-\infty }^{\infty }x(t)e^{-j\omega t}\,dt.$

將$x(t)$進行上述的替換：

$X(\omega )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau \right]\,e^{-j\omega t}\,dt$

$=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,d\tau \,dt.$

將積分順序進行交換：

$X(\omega )=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\,d\tau$

$=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\right]\,d\tau$

$=\int _{-\infty }^{\infty }X(\tau ,\omega )\,d\tau .$

因此傅利葉轉換可以視為某種將$x(t)$所有的短時距傅利葉轉換的相位同調部分進行相加。

而反傅利葉轉換公式如下：

$x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\omega )e^{+j\omega t}\,d\omega ,$

因此 $x(t)$可以從$X(\tau ,\omega )$被復原

$x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\tau \,d\omega .$

或

$x(t)=\int _{-\infty }^{\infty }\left[{\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega \right]\,d\tau .$

與上面所列的窗函數的式子進行比較，可得

$x(t)w(t-\tau )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega .$

對反傅利葉轉換公式中的$X(\tau ,\omega )$來說$\tau$是不變的

$x(t)=w(t_{1}-t)^{-1}\int _{-\infty }^{\infty }X(t_{1},f)e^{j2\pi ft}\,df;\ \ w(t_{1}-t)\neq 0$

另外用角頻率來表示：

$x(t)={\frac {1}{2\pi }}w^{-1}(t_{1}-t)\int \limits _{-\infty }^{\infty }X(t_{1},w)e^{jwt}dw$

窗函數

窗函數通常滿足下列特性:

1. $w(t)=w(-t)\,$，即為偶函數。
2. $max(w(t))=w(0)\,$，即窗函數的中央通常是最大值的位置。
3. $w(t_{1})\geq w(t_{2}),|t_{2}|\geq |t_{1}|$，即窗函數的值由中央開始向兩側單調遞減。
4. $w(t)\cong 0,|t|\to \infty$，即窗函數的值向兩側遞減為零。

常見的窗函數有：方形、三角形、高斯函數等，而短時距傅利葉轉換也因窗函數的不同而有不同的名稱。而加伯轉換，即為窗函數是高斯函數的短時距傅利葉轉換，通常沒有特別說明的短時距傅利葉轉換，即為加伯轉換。

非對稱窗函數

當在特殊應用時，窗函數特性的第一點可以不滿足，如下圖的非對稱窗函數$w(t)$，其中$B_{1}\neq B_{2}$。左圖為窗函數原本的圖形，而在計算短時距傅利葉變換時，需將窗函數轉到$\tau$軸上得出$w(t-\tau )$，換言之，欲得到的短時距傅利葉變換的結果需在$t+B_{1}$的時間點才能算出，因此若$B_{1}$愈小，即可愈快得結果，此種非對稱窗函數可應用在地震波、碰撞偵測...等，需要即時處理的應用。

優缺點

• 優點：比起傅利葉轉換更能觀察出訊號瞬時頻率的資訊。
• 缺點：計算複雜度高

方形窗函數的短時距傅利葉轉換

概念

方形窗函數，B = 50，橫軸為時間(秒)

右圖即為方形窗函數的一個例子，其數學定義： $w(t)={\begin{cases}\ 1;&|t|\leq B\\\ 0;&|t|>B\end{cases}}$

可以隨要分析的訊號，來調整B的大小（即調整方形窗函數的寬度）。至於B的選擇，將會在下面探討。

短時傅利葉轉換可以簡化為

$X(t,f)=\int _{t-B}^{t+B}x(\tau )e^{-j2\pi f\tau }\,d\tau$

反短時傅利葉轉換可簡化為

$x(t)=\int _{-\infty }^{\infty }X(t_{1},f)e^{j2\pi ft}\,df;t-B<t_{1}<t+B$

特性

其大部分的特性都與傅利葉轉換的特性相對應

• 積分特性

$\int _{-\infty }^{\infty }X(t,f)\,df=\int _{t-B}^{t+B}x(\tau )\int _{-\infty }^{\infty }e^{-j2\pi f\tau }\,df\,d\tau ={\begin{cases}\ x(0);&|t|\leq B\\\ 0;&|t|>B\end{cases}}$

• 位移特性(時間軸方向的移動)

$\int _{t-B}^{t+B}x(\tau +\tau _{0})e^{-j2\pi f\tau }\,d\tau =X(t+\tau _{0},f)e^{j2\pi f\tau _{0}}$

• 調變特性(頻率軸方向的移動)

$\int _{t-B}^{t+B}\left(x(\tau )e^{j2\pi f_{0}\tau }\right)e^{-j2\pi f\tau }\,d\tau =X(t,f-f_{0})$

• 線性特性

若有一訊號$h(t)=\alpha x(t)+\beta y(t)\,$，$H(t,f),X(t,f),Y(t,f)\,$分別為$h(t),x(t),y(t)\,$做方形窗函數短時 距傅利葉轉換的結果，則$H(t,f)=\alpha X(t,f)+\beta Y(t,f)\,$。

• 能量積分特性

$\int _{-\infty }^{\infty }|X(t,f)|^{2}\,df=\int _{t-B}^{t+B}|x(\tau )|^{2}\,d\tau$

$\int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df=\int _{t-B}^{t+B}x(\tau )y^{*}(\tau )\,d\tau$

• 特殊訊號

1. 當$x(t)=\delta (t)\,$，

$X(t,f)={\begin{cases}\ 1;&|t|\leq B\\\ 0;&|t|>B\end{cases}}$

2. 當$x(t)=1\,$，

$X(t,f)=2Bsinc(2Bf)e^{-j2\pi ft}\,$

方形窗函數寬度$(B)$的選取

方形窗函數短時距傅利葉轉換用不同窗函數寬度(B)的比較，橫軸為時間(秒)，縱軸為頻率(赫茲)

• 由上述特性中的特殊訊號$x(t)=\delta (t)$來分析，訊號只有在$t=0$的時候有值；若短時距傅利葉轉換是理想的話，$X(t,f)$應該只有在$t=0$的時候有能量。但由上面的特性可發現，能量會出現在${\begin{smallmatrix}|t|\leq B\end{smallmatrix}}$中間。因此，若我們取較小的$B$，則可使結果趨近理想。
• 接着我們來分析$x(t)=1$，訊號因為沒有改變，應該為DC。若短時距傅利葉轉換是理想的話，$X(t,f)$應該只有在$f=0$的時候有能量。但由上面的特性可發現，能量會沿着頻率軸呈現sinc函數。若我們取較大的$B$，可使sinc函數沿着頻率軸變窄，使得結果趨近理想。
• 綜合以上說明，若我們使用較大的方形窗函數寬度$(B)$，則$X(t,f)$時間軸的解像度會下降；頻率軸的解像度上升。若使用較小的$B$，則$X(t,f)$時間軸的解像度會上升；頻率軸的解像度下降。我們以下面做為例子說明：

$x(t)={\begin{cases}\cos(2\pi t);&t<10\\\cos(6\pi t);&10\leq t<20\\\cos(4\pi t);&t\geq 20\end{cases}}$

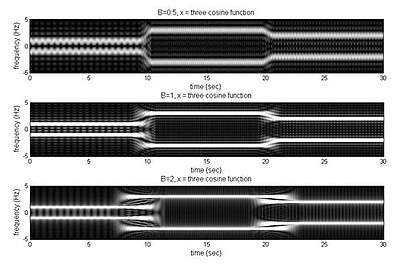
結果如右圖所示，B越大則在頻率變化處(t = 10, 20)附近的頻率越不準確，即可能會有多個頻率成分出現。但同時，其他時間點的能量則較集中；沒有如B較小時，頻率散開或模糊的情形。

上述也是其中一個小波轉換及多解像度分析作為改進的方向，其中多解像度分析能在高頻時有較好的時間軸解析，而在低頻時能有較好的頻率軸解析，此種組合較契合許多實際的應用。

時間軸與頻率軸的解像度無法同時提升也與海森堡不確定性原理有關，即時間與頻率的標準差乘積有所限制，而高斯函數恰好能符合不確定性原理的極值，也就是兩者同時達到最好的解像度，而應用高斯函數的時頻分析方法即為加伯轉換，而在經過修改及多解像度分析後，成為了莫萊小波。

優缺點

• 優點：方形窗函數的短時距傅利葉轉換有許多可應用的數學特性，在數碼的應用上所需的計算時間較少。
• 缺點：時頻分析的表現較差

其他窗函數

高斯窗函數

概念

高斯窗函數的短時距傅利葉轉換又稱為加伯轉換。以下是高斯函數的數學定義，

$w(t)=\exp(-\pi \sigma t^{2})$

據此，短時傅利葉轉換可以寫為

$G_{x}(t,f)=\int _{-\infty }^{\infty }e^{-\pi (\tau -t)^{2}}e^{-j2\pi f\tau }x(\tau )d\tau$

優缺點

• 優點：可以在時間跟頻率上有更好的平衡，得到較清楚的時頻圖。
• 缺點：因窗函數跟訊號本身的乘法，計算時間跟複雜度都比較高。

三角形窗函數

三角形函數，橫軸為時間，B=1/2

概念

三角形窗函數如右圖所示，數學定義如下，

$w(t)=max(1-\left\vert t\right\vert ,0)$

$w(t)={\begin{cases}1-\left\vert t\right\vert ,&\left\vert t\right\vert <2B;\\0,&{\text{otherwise.}}\end{cases}}$

可使用在震幅改變的情況下，相對於方形窗函數，可更好的濾除雜訊。

海寧(Hanning/ Hann)窗函數

海寧函數

概念

海寧函數如右圖所示，數學定義如下，

$w(t)={\begin{cases}0.5+0.5cos(\pi t/B),&{\text{when }}\left\vert t\right\vert \leq B\\0,&{\text{otherwise }}\end{cases}}$

相較於三角形窗函數，海寧窗函數更為貼近現實訊號的趨勢，可進一步濾除雜訊。

漢明(Hamming)窗函數

漢明函數

概念

漢明窗函如右圖所示，數學定義如下，

$w(t)={\begin{cases}0.54+0.46cos(\pi t/B),&{\text{when }}\left\vert t\right\vert \leq B\\0,&{\text{otherwise }}\end{cases}}$

跟海寧窗函數類似，但兩端不為零。

海寧與漢明窗的區別

窗函數有四個指標，分別為

• 泄露指數 (Leakage Factor)
• 主辦寬度 (Mainlobe width)
• 旁辦衰減 (Sidelobe attenuation)
• 旁辦滾降率 (Sidelobe roll-off rate)

  

  方形窗函數寬度(B)與STFT清晰率的取捨，橫軸為時間(秒)，縱軸為頻率(赫茲)

因為漢明窗兩端不能到零，而海寧窗兩端為零。從以上頻率響應來看，漢明窗可以有效減少靠近的旁辦，但在較遠的旁辦洩漏比海寧窗嚴重。

如何決定窗函數

可根據以下條件來選取窗函數，

• 複雜度，方形複雜度較低
• 解析率，以方形為例，越寬的主辦可以得到更清楚的時頻圖，卻會把雜訊也一同顯示，反之則得到不清晰的時頻圖

在決定複雜度跟解析率後，可利用不同的窗函數達到更好的濾雜訊效果。

瑞利頻率

當Nyquist頻率是能被有意義分析的頻率最大值的限制，而瑞利頻率則是能被有限頻寬頻的窗函數解析的頻率最小值的限制。若給定一窗函數的長度是T秒，最低能被解析的頻率即為1/T Hz。

瑞利頻率在短時距傅利葉變化的應用中扮演重要的角色，像是在分析神經訊號時。

頻譜(Spectrogram)

Spectrogram即短時傅利葉轉換後結果的絕對值平方，兩者本質上是相同的，在文獻上也常出現spectrogram這個名詞。

$SP_{x}(t,f)=|X(t,f)|^{2}=|\int _{-\infty }^{\infty }w(t-\tau )x(\tau )e^{-j2\pi f\tau }\,d\tau |^{2}$

應用

應用短時距傅利葉變換分析聲音訊號

短時距傅利葉變換及其他工具經常用於分析音樂。

如右圖所示，

1. 水平軸為頻率，左側為最低頻率，右側為最高頻率
2. 條形高度(混和顏色表示)表示該頻帶內的頻率幅度
3. 深度表示時間

音頻工程師使用這種視覺來獲取有關音頻樣本的資訊。

此外，因頻率會隨時間而改變，短時距也可使用在以下情境，

• 訊號取樣 (signal sampling)，
• 調變 (modulation)，
• 生物訊號 (biomedical signals)，等等

若與時間無關，如卷積，照片等則不能使用短時距傅利葉變換來進行分析。而影片屬於3D訊號，其短時距傅利葉產物為6D訊號，故也不適用。

短時距傅利葉變換實現方法

從連續短時距傅利葉變化的定義出發

${X}\left({t,f}\right)=\int _{-\infty }^{\infty }{w\left({t-\tau }\right)\cdot }{x}\left({\tau }\right)\,{e^{-j2\pi \,f\tau }}\cdot d\tau$

令 $t=n\Delta _{t},f=m\Delta _{f},\tau =p\Delta _{t}$ ，則上述式子時域可從連續轉為離散

${X}\left({n{\Delta _{t}},m{\Delta _{f}}}\right)=\sum \limits _{p=-\infty }^{\infty }{w\left({(n-p){\Delta _{t}}}\right){x}\left({p{\Delta _{t}}}\right)}{e^{-j2\pi \,mp{\Delta _{t}}{\Delta _{f}}}}{\Delta _{t}}$

若當$\left|t\right|>B,w(t)\cong 0\qquad {\frac {B}{\Delta _{t}}}=Q$

上式可改寫為

${X}\left({n{\Delta _{t}},m{\Delta _{f}}}\right)=\sum \limits _{p=n-Q}^{n+Q}{w\left({(n-p){\Delta _{t}}}\right){x}\left({p{\Delta _{t}}}\right)}{e^{-j2\pi \,mp{\Delta _{t}}{\Delta _{f}}}}{\Delta _{t}}$

---

直接運算

限制條件

(1)要滿足Nyquist criterion

${\Delta _{t}}<{\frac {1}{2\Omega }}\qquad {\Omega }={{\Omega _{x}}+{\Omega _{w}}}$

$x(\tau )$的頻寬為$\Omega _{x}$。而$w(\tau )$的頻寬則為$\Omega _{w}$，$w(t-\tau )$的頻寬也為$\Omega _{w}$

因為在時域相乘相當於在頻域做摺積，因此$x(\tau )w(t-\tau )$的頻寬為$\Omega _{x}+\Omega _{w}$(通常$\Omega _{x}$會遠大於$\Omega _{w}$，所以主要影響頻寬的是$\Omega _{x}$)

推導

$X(t,f)=\int _{-\infty }^{\infty }w(t-\tau )x(\tau )e^{-j2\pi f\tau }d\tau$

轉換到離散形式($t=n\Delta _{t},f=m\Delta _{f},\tau =p\Delta _{t}$)，其中$\Delta _{t}={\frac {1}{f_{s}}}$

$X(n\Delta _{t},m\Delta _{f})=\sum _{p=-\infty }^{\infty }w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j2\pi pm\Delta _{t}\Delta _{f}}\Delta _{t}$，由於無限大的上下限實務上做不到，所以嘗試變成有限大的上下限。

假設$w(t)\cong 0$ for $|t|>B,{\frac {B}{\Delta _{t}}}=Q$

$X(n\Delta _{t},m\Delta _{f})=\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j2\pi pm\Delta _{t}\Delta _{f}}\Delta _{t}$

• 對於縮放的加伯轉換，$Q={\frac {1.9143}{{\sqrt {\sigma }}\Delta t}}$

時間複雜度

$TF(2Q+1)\to O(TFQ)$

假設t-axis有T個取樣點，f-axis有F個取樣點，則我們總共要對TF個點做$(2Q+1)$次的運算，因此可得複雜度為$TF(2Q+1)$

優缺點

優點：簡單及有彈性(因為限制少)

缺點：複雜度較高

---

快速傅利葉變換

限制條件

(1)要滿足Nyquist criterion

${\Delta _{t}}<{\frac {1}{2\Omega }}\qquad {\Omega }={{\Omega _{x}}+{\Omega _{w}}}$

(2)${\Delta _{t}}{\Delta _{f}}={\textstyle {1 \over {N}}}$ (N可為任意整數)

(3) $N\geq 2Q+1$ (做N點傅利葉轉換，輸入必要<=N)

推導

標準的離散傅利葉轉換式子為

$Y[m]=\sum \limits _{n=0}^{N-1}y[n]e^{-j{\frac {2\pi mn}{N}}}$

由直接運算得知如下公式

${X}\left({n{\Delta _{t}},m{\Delta _{f}}}\right)=\sum \limits _{p=n-Q}^{n+Q}{w\left({(n-p){\Delta _{t}}}\right){x}\left({p{\Delta _{t}}}\right)}{e^{-j2\pi \,mp{\Delta _{t}}{\Delta _{f}}}}{\Delta _{t}}$

因此為了讓上式符合離散傅利葉轉換的上下界，令$q=p-(n-Q)\to p=(n-Q)+q$代入上式即可得

${X}\left({n{\Delta _{t}},m{\Delta _{f}}}\right)={\Delta _{t}}{e^{j{\textstyle {{2\pi \,(Q-n)m} \over N}}}}\sum \limits _{q=0}^{N-1}{x_{1}\left({q}\right){e^{-j{\textstyle {{2\pi \,qm} \over N}}}}}$

其中 ${\begin{cases}{x_{1}}\left(q\right)=w\left({(Q-q){\Delta _{t}}}\right)x\left({(n-Q+q){\Delta _{t}}}\right),&{\mbox{for}}{\rm {0}}\leq q\leq 2{\rm {Q}}\\{x_{1}}\left(q\right)=0,&{\mbox{for}}{\rm {2}}Q<q\leq N\end{cases}}$

運算步驟

假設$t=n_{0}\Delta _{t},(n_{0}+1)\Delta _{t},\cdots \cdots ,(n_{0}+T-1)\Delta _{t}$

$\,f=m_{0}\Delta _{f},(m_{0}+1)\Delta _{f},\cdots \cdots ,(m_{0}+F-1)\Delta _{f}$

步驟一：計算$n_{0},m_{0},T,F,N,Q$

步驟二：$n=n_{0}$

步驟三：決定$x_{1}(q)$

步驟四：$X_{1}(m)=FFT[x_{1}(q)]$

步驟五：轉換$X_{1}(m)$成$X(n\Delta _{t},m\Delta _{f})$

步驟六：設$n=n+1$，並回到步驟三，直到$n=n_{0}+T+1$

• 範例

${\begin{cases}x(t)=\cos {(2\pi t)},&{\mbox{when }}t<10\\x(t)=\cos {(6\pi t)},&{\mbox{when }}10\leq t<20\\x(t)=\cos {(4\pi t)},&{\mbox{when }}t\geq 20\\\end{cases}}$

藉由取樣定理可得知$\Delta _{t}<{\frac {1}{6}}$

假設$f=-5\sim 5$及$\Delta _{f}=0.1$，則經由$f=m\Delta _{f}$可得$m=-50\sim 50$

$\;t=0\sim 30$及$\Delta _{t}=0.1$，則經由$t=n\Delta _{t}$可得$n=0\sim 300$

步驟一：$n_{0}=0,m_{0}=-50,T=301,F=101,N={\frac {1}{\Delta _{t}\Delta _{f}}}=100,Q={\frac {B}{\Delta _{t}}}=10$

步驟二：$n=n_{0}=0$

步驟三：計算$x_{1}(q)(q=0\sim 99)$

步驟四：利用求得的$x_{1}(q)$計算快速傅利葉轉換 $X_{1}[m]=\sum _{q=0}^{N-1}x_{1}(q)e^{-j{\frac {2\pi qm}{N}}}$

步驟五：轉換$X_{1}(m)$到$X(n\Delta _{t},m\Delta _{f})$

$X(n\Delta _{t},m\Delta _{f})=X_{1}[m]\Delta _{t}e^{j{\frac {2\pi (Q-n)m}{N}}}$

• 註：若是於程式中執行，要注意m可能為負數，所以需要利用到週期性性質$X_{1}[m]=X_{1}[m+N]$

$X_{1}[-50]=X_{1}[50],X_{1}[-49]=X_{1}[51],\cdots \cdots ,X_{1}[-1]=X_{1}[99]$

因此可將上式改為$X(n\Delta _{t},m\Delta _{f})=X[((m))_{N}]e^{j{\frac {2\pi (Q-n)m}{N}}}$，其中$((m))_{N}$代表取m除以N的餘數

步驟六：設定$n=n+1$，回到步驟三直到$n=n_{0}+T-1$

時間複雜度

利用FFT計算$\sum \limits _{q=0}^{N-1}{x_{1}\left({q}\right){e^{-j{\textstyle {{2\pi \,qm} \over N}}}}}$，其中每次FFT的時間複雜度為 $N{\log _{2}}N$

總時間複雜度為$TN{\log _{2}}N\to O(TN{\log _{2}}N)$

優缺點

優點：與直接運算相比，複雜度較低

缺點：較多限制，包括 ${\begin{cases}\Delta _{t}<{\frac {1}{2(\Omega _{x}+\Omega _{w})}}\\\Delta _{t}\Delta _{f}={\frac {1}{N}}\\N\geq 2Q+1\\\end{cases}}$

---

使用快速傅利葉變換加上遞迴關係式

限制條件

(1)要滿足Nyquist criterion

${\Delta _{t}}\leq {\frac {1}{2\Omega }}\qquad {\Omega }={{\Omega _{x}}+{\Omega _{w}}}$

(2)${\Delta _{t}}{\Delta _{f}}={\textstyle {1 \over {N}}}$

(3)$N\geq 2Q+1$

(4)需為方形窗函數的短時距傅利葉轉換

推導

因為是方形窗函數 ${w}\left((n-p){\Delta _{t}}\right)=1$，因此原式可由此關係變成以下式子

${X}\left({n{\Delta _{t}},m{\Delta _{f}}}\right)=\sum \limits _{p=n-Q}^{n+Q}{{x}\left({p{\Delta _{t}}}\right)}{{w}\left((n-p){\Delta _{t}}\right)}{e^{-j2\pi \,mp{\Delta _{t}}{\Delta _{f}}}}{\Delta _{t}}\to {X}\left({n{\Delta _{t}},m{\Delta _{f}}}\right)=\sum \limits _{p=n-Q}^{n+Q}{{x}\left({p{\Delta _{t}}}\right)}{e^{-j2\pi \,mp{\Delta _{t}}{\Delta _{f}}}}{\Delta _{t}}$

而由此可看出n和n-1有遞迴關係，如下

${X}\left({(n-1){\Delta _{t}},m{\Delta _{f}}}\right)=\sum \limits _{p=n-1-Q}^{n-1+Q}{{x}\left({p{\Delta _{t}}}\right)}{e^{-j2\pi \,mp{\Delta _{t}}{\Delta _{f}}}}{\Delta _{t}}={X}\left({n{\Delta _{t}},m{\Delta _{f}}}\right)+x((n-Q-1)\Delta _{t})-x((n+Q+1)\Delta _{t})$

(1)以FFT計算${X}\left({{n_{0}}{\Delta _{t}},m{\Delta _{f}}}\right)={\Delta _{t}}{e^{j{\textstyle {{2\pi \,(Q-n_{0})m} \over N}}}}\sum \limits _{q=0}^{N-1}{x_{1}\left({q}\right){e^{-j{\textstyle {{2\pi \,qm} \over N}}}}}\qquad {n_{0}}=min(n)$

其中${\begin{cases}{x_{1}}\left(q\right)=x\left({(n-Q+q){\Delta _{t}}}\right),&{\mbox{for}}{\rm {0}}\leq q\leq 2{\rm {Q}}\\{x_{1}}\left(q\right)=0,&{\mbox{for}}{q>2{\rm {Q}}}\end{cases}}$

(2)利用遞迴關係式計算算${X}\left({{n}{\Delta _{t}},m{\Delta _{f}}}\right),\qquad n={n_{0}}+1\backsim max(n)$

則${X}\left({{n_{0}}{\Delta _{t}},m{\Delta _{f}}}\right)={X}\left({(n-1){\Delta _{t}},m{\Delta _{f}}}\right)-{x}\left((n-Q-1){\Delta _{t}}\right){e^{-j{\textstyle {{2\pi \,(n-Q-1)m} \over N}}}}{\Delta _{t}}+{x}\left((n+Q){\Delta _{t}}\right){e^{-j{\textstyle {{2\pi \,(n+Q)m} \over N}}}}{\Delta _{t}}$

時間複雜度

(1)FFT計算一次 ${X}\left({{n_{0}}{\Delta _{t}},m{\Delta _{f}}}\right)={\Delta _{t}}{e^{j{\textstyle {{2\pi \,(Q-n_{0})m} \over N}}}}\sum \limits _{q=0}^{N-1}{x_{1}\left({q}\right){e^{-j{\textstyle {{2\pi \,qm} \over N}}}}}\qquad {n_{0}}=min(n)$

• 時間複雜度：$O(N\log _{2}N)$

(2)利用遞迴關係，計算$n=n_{0}+1$時的數值，因此共會執行T-1次遞迴，如下式

${X}\left({{n_{0}}{\Delta _{t}},m{\Delta _{f}}}\right)={X}\left({(n-1){\Delta _{t}},m{\Delta _{f}}}\right)-{x}\left((n-Q-1){\Delta _{t}}\right){e^{-j{\textstyle {{2\pi \,(n-Q-1)m} \over N}}}}{\Delta _{t}}+{x}\left((n+Q){\Delta _{t}}\right){e^{-j{\textstyle {{2\pi \,(n+Q)m} \over N}}}}{\Delta _{t}}$

每次遞迴都要計算${x}\left((n-Q-1){\Delta _{t}}\right){e^{-j{\textstyle {{2\pi \,(n-Q-1)m} \over N}}}}{\Delta _{t}}$及${x}\left((n+Q){\Delta _{t}}\right){e^{-j{\textstyle {{2\pi \,(n+Q)m} \over N}}}}{\Delta _{t}}$兩個乘法(相當於2F的複雜度)

• 時間複雜度：$2F(T+1)\to O(TF)$

總時間複雜度 $2(T-1)F+N{\log _{2}}N\to O(FT)$

優缺點

優點：四種運算中，最低的複雜度$O(TF)$

缺點：

1. 只適用於方形窗函數的短時傅利葉轉換
2. 由於遞迴的關係，會有累加誤差。所以只要當中有小錯誤，誤差會累積到最後，造成無可預期的錯誤
3. 不能用在不平衡的取樣點

---

使用Chirp-Z 轉換

限制條件

(1)要滿足Nyquist criterion

${\Delta _{t}}\leq {\frac {1}{2\Omega }}\qquad {\Omega }={{\Omega _{x}}+{\Omega _{w}}}$

推導

令$exp(-j2\pi \,mp{\Delta _{t}}{\Delta _{f}})=exp(-j\pi \,p^{2}{\Delta _{t}}{\Delta _{f}})exp(j\pi \,{(p-m)}^{2}{\Delta _{t}}{\Delta _{f}})exp(-j\pi \,m^{2}{\Delta _{t}}{\Delta _{f}})$

即可由直接運算的式子導出Chirp_Z變換的式子，如下所示

${X}\left({n{\Delta _{t}},m{\Delta _{f}}}\right)={\Delta _{t}}\sum \limits _{p=n-Q}^{n+Q}{w\left({(n-p){\Delta _{t}}}\right){x}\left({p{\Delta _{t}}}\right)}{e^{-j2\pi \,mp{\Delta _{t}}{\Delta _{f}}}}\to {X}\left({n{\Delta _{t}},m{\Delta _{f}}}\right)={\Delta _{t}}{e^{-j\pi \,m^{2}{\Delta _{t}}{\Delta _{f}}}}\sum \limits _{p=n-Q}^{n+Q}{w\left({(n-p){\Delta _{t}}}\right){x}\left({p{\Delta _{t}}}\right)}{e^{-j\pi \,p^{2}{\Delta _{t}}{\Delta _{f}}}}{e^{j\pi \,{(p-m)}^{2}{\Delta _{t}}{\Delta _{f}}}}$

運算步驟

Step1:$x_{1}[p]=w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j\pi p^{2}\Delta _{t}\Delta _{f}}$ $\quad \quad n-Q\leq p\leq n+Q$

Step2:$X_{2}[n,m]=\sum _{p=n-Q}^{n+Q}x_{1}[p]c[m-p]\quad \quad c[m]=e^{j\pi m^{2}\Delta _{t}\Delta _{f}}$

Step3:$X(n\Delta _{t},m\Delta _{f})=\Delta _{t}e^{-j\pi m^{2}\Delta _{t}\Delta _{f}}X_{2}[m,n]$

時間複雜度

當n為定值時

(1)假設$x_{1}[p]=w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j\pi p^{2}\Delta _{t}\Delta _{f}}\to$ 相乘時間複雜度為2Q+1

(2)令$c[m]=e^{j\pi m^{2}\Delta _{t}\Delta _{f}}$，則$\sum \limits _{p=n-Q}^{n+Q}x_{1}[p]c[m-p]\to$ convolution時間複雜度為 $3N{\log _{2}}N$

(3)${\Delta _{t}}{e^{-j\pi \,m^{2}{\Delta _{t}}{\Delta _{f}}}}\sum \limits _{p=n-Q}^{n+Q}{w\left({(n-p){\Delta _{t}}}\right){x}\left({p{\Delta _{t}}}\right)}{e^{-j\pi \,p^{2}{\Delta _{t}}{\Delta _{f}}}}{e^{j\pi \,{(p-m)}^{2}{\Delta _{t}}{\Delta _{f}}}}\to$相乘時間複雜度為 F

因此，總時間複雜度為$T(2Q+1+F+3N{\log _{2}}N)\to O(TN{\log _{2}}N)$

雖然此實現方法和使用FFT計算的時間複雜度相同，但因為convolution相當於做三次FFT，因此實際操作時運算時間約為使用FFT計算的2~3倍

優缺點

優點：只有一項限制：$\Delta _{t}<{\frac {1}{2(\Omega _{x}+\Omega _{w})}}$

缺點：與前四種相比，複雜度是中間的。

---

Unbalanced Sampling for STFT and WDF

將直接法和快速傅利葉轉換方法做修正

1.直接法

$X(t,f)=\int _{-\infty }^{\infty }w(t-\tau )x(\tau )e^{-j2\pi f\tau }d\tau$

修正後 ：$X(n\Delta _{t},m\Delta _{f})=\sum _{p=nS-Q}^{nS+Q}w((nS-p)\Delta _{\tau })x(p\Delta _{\tau })e^{-j2\pi pm\Delta _{\tau }\Delta _{f}}\Delta _{\tau }$

其中， $t=n\Delta _{t},f=m\Delta _{f},\tau =p\Delta _{\tau },B=Q\Delta _{\tau }$ ,$S={\frac {\Delta _{t}}{\Delta _{\tau }}},\Delta _{t}\neq \Delta _{\tau }$

假設$w(t)\approxeq 0$ for $|t|>B$，則上下限可藉由以下推導而修正

$\int _{t+B}^{t-B}\to \int _{n\Delta _{t}+Q\Delta _{\tau }}^{n\Delta _{t}-Q\Delta _{\tau }}$ 則上限可以寫成$n\Delta _{t}+Q\Delta _{\tau }==nS\Delta _{\tau }+Q\Delta _{\tau }=\Delta _{\tau }(nS+Q)$，下限則以此類推

註：$\Delta _{\tau }$(輸入訊號的取樣間隔)

$\Delta _{t}$(在t軸上的輸出訊號的取樣間隔)

然而，$S={\frac {\Delta _{t}}{\Delta _{\tau }}}$是整數會是比較好的。

• 假設一聲音訊號：

${\begin{cases}\Delta _{\tau }={\frac {1}{44100}}\\\Delta _{t}={\frac {1}{100}}\end{cases}}$ 則經由上述公式可求得S=441，代表經由unbalanced sampling，我們跟原本$\Delta _{t}=\Delta _{\tau }={\frac {1}{44100}}$相比可減少441倍的取樣點。

時間複雜度

由於t軸的取樣點少了S倍，因此跟原本的直接運算複雜度相比，只要把$T\to {\frac {T}{S}}$即可，如下：

複雜度：$O({\frac {T}{S}}N\log _{2}N)$

2.快速傅利葉轉換

限制條件

(1) $\Delta _{\tau }\Delta _{f}={\frac {1}{N}}$

(2) $N={\frac {1}{\Delta _{\tau }\Delta _{f}}}>2Q+1$ : ($\Delta _{\tau }\Delta _{f}$只要是整數的倒數即可)

(3) $\Delta _{\tau }<{\frac {1}{2\Omega }}$，$w(\tau -t)x(\tau )$的頻寬是 $\Omega$

i.e. $|FT\{w(\tau -t)x(\tau )\}|=|X(t,f)|\approx 0$ ，當 $|f|>\Omega$

過程

$X(n\Delta _{t},m\Delta _{f})=\sum _{p=nS-Q}^{nS+Q}w((nS-p)\Delta _{\tau })x(p\Delta _{\tau })e^{-j{\tfrac {2\pi pm}{N}}}\Delta _{\tau }$

令 $q=p-(nS-Q)\longrightarrow p=(nS-Q)+q$

$x_{1}(q)=w((Q-q)\Delta _{\tau })x((nS-Q+q)\Delta _{\tau })$ for $0\leq q\leq 2Q$

$x_{1}(q)=0\qquad \qquad \qquad \qquad \qquad \qquad \quad \quad$for $2Q<q<N$

修正後：$X(n\Delta _{t},m\Delta _{f})=\Delta _{\tau }e^{j{\tfrac {2\pi (Q-nS)m}{N}}}\sum _{q=0}^{N-1}x_{1}(q)e^{-j{\tfrac {2\pi qm}{N}}}$

運算步驟

假設$t=c_{0}\Delta _{t},(c_{0}+1)\Delta _{t},\cdots ,(c_{0}+C-1)\Delta _{t}=c_{0}S\Delta _{\tau },(c_{0}S+S)\Delta _{\tau },\cdots ,[c_{0}S+(C-1)S]\Delta _{\tau }$

$\quad \;\;f=m_{0}\Delta _{f},(m_{0}+1)\Delta _{f},\cdots ,(m_{0}+F-1)\Delta _{f}$

$\quad \;\;\tau =n_{0}\Delta _{\tau },(n_{0}+1)\Delta _{\tau },\cdots ,(n_{0}+T-1)\Delta _{\tau }$

步驟一：計算$c_{0},m_{0},n_{0},C,F,T,N,Q$

步驟二：$n=c_{0}$

步驟三：決定$x_{1}(q)$

步驟四：$X_{1}(m)=FFT[x_{1}(q)]$

步驟五：轉換$X_{1}(m)\to X(n\Delta _{t},m\Delta _{f})$

步驟六：設定$n=n+1$及返回步驟三，直到$n=c_{0}+C-1$

複雜度

$O({\frac {T}{S}}N\log _{2}N)$

Non-Uniform $\Delta _{t}$

(1) 先用比較大的$\Delta _{t}$

(2) 如果發現$|X(n\Delta _{t},m\Delta _{f})|$ 和 $|X((n+1)\Delta _{t},m\Delta _{f})|$ 之間有很大的差異，則在$n\Delta _{t}$，$(n+1)\Delta _{t}$ 之間選用比較小的取樣區間$\Delta _{t1}$

($\Delta _{\tau }<\Delta _{t1}<\Delta _{t}$，${\frac {\Delta _{t}}{\Delta _{t1}}}$ 和 ${\frac {\Delta _{t1}}{\Delta _{\tau }}}$皆為整數)

再用Unbalanced Sampling for STFT and WDF 中修正後的快速傅利葉轉換方法算出 $X(n\Delta _{t}+\Delta _{t1},m\Delta _{f})$，$X(n\Delta _{t}+2\Delta _{t1},m\Delta _{f})$$X((n+1)\Delta _{t}-\Delta _{t1},m\Delta _{f})$

(3) 以此類推，如果 $|X(n\Delta _{t}+k\Delta _{t1},m\Delta _{f})|,|X((n+1)\Delta _{t}+(k+1)\Delta _{t1},m\Delta _{f})|$的差距還是太大，則再選用更小的取樣間隔$\Delta _{t2}$

($\Delta _{\tau }<\Delta _{t2}<\Delta _{t1}$，${\frac {\Delta _{t1}}{\Delta _{t2}}}$ 和 ${\frac {\Delta _{t2}}{\Delta _{\tau }}}$皆為整數)

• 比較

若有一音樂訊號總共有1.6秒，$\Delta _{\tau }={\frac {1}{44100}}$

1. 選擇$\Delta _{t}=\Delta _{\tau }$，則共有$44100*1.6+1=70561$點
2. 選擇$\Delta _{t}=0.01=441\Delta _{\tau }$，則共有$100*1.6+1=161$點
3. t隨時間不同有不同的選擇，如下

$t=0,0.05,0.1,0.15,0.2,0.4,0.45,0.46,0.47,0.48,0.49,0.5,0.55,0.6,0.8,0.85,0.9,0.95,0.96,0.97,0.98,0.99,1,1.05,1.1,1.15,1.2,1.4,1.6$，共29點

可以這樣做的原因為：有些音樂訊號在和弦與和弦中間幾乎沒有變化，因此可以挑選較大的$\Delta _{t}$取樣;和弦在變換時，頻率會變化的較劇烈，因此變換和弦是需要用較多的取樣點。藉由此種non-uniform的取樣，可以讓我們大幅減少運算量，從最一開始的$70561\to 29$可看出我們的運算量大幅降低。

參見

• 閔可夫斯基空間
• 柯西不等式
• 三角不等式
• 完備空間

參考書目、資料來源

1. Jian-Jiun Ding, Time frequency analysis and wavelet transform class notes, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2011.
2. Alan V. Oppenheim, Ronald W. Schafer, John R. Buck : Discrete-Time Signal Processing, Prentice Hall, ISBN 0-13-754920-2
3. Jian-Jiun Ding, Time frequency analysis and wavelet transform class notes, Graduate Institute of Communication Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2017.
4. Jian-Jiun Ding, Time frequency analysis and wavelet transform class notes, Graduate Institute of Communication Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2020.
5. Jian-Jiun Ding, Time frequency analysis and wavelet transform class notes, Graduate Institute of Communication Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2022.