討論:反餘切
外觀
|
本條目依照頁面評級標準評為丙級。 本條目屬於下列維基專題範疇: |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||
| 反餘切曾於2014年8月12日通過新條目推薦投票,登上維基百科首頁的「你知道嗎?」欄位。 |
 | 此條目為第十二次動員令大動員令的作品之一,而此條目是一篇達標條目。 |
新條目推薦討論

- 哪一種反三角函數在三角測量學與複變分析中擁有不同的定義且在x<0時兩者的定義差了一個圓周率?
- (+)支持--Banyangarden(留言) 2014年8月7日 (四) 13:48 (UTC)
- (!)意見--答案唯一嗎?六種三角函數反函數的任一種在三角測量學與複變分析中都擁有不同的定義吧!?克勞棣 2014年8月7日 (四) 15:12 (UTC)
- 然後
- 你會發現裏面只有反餘切不一樣。因此問題應該唯一了--宇帆(留言·聯絡) 2014年8月7日 (四) 16:09 (UTC)
- (+)支持--Wolfch (留言)-DC12, 基礎條目 2014年8月7日 (四) 22:51 (UTC)
- (+)支持--SSR2000(留言) 2014年8月8日 (五) 16:04 (UTC)
- (+)支持--Iflwlou [ M { 2014年8月8日 (五) 16:59 (UTC)
到達域
[編輯]如果我沒理解錯的話,應該是
- 函數2:(0,π)
- 函數3:(-π/2,π/2]
這樣? --578985s(留言) 2014年8月12日 (二) 07:14 (UTC)
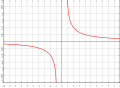
- (:)回應,@ㄑㄑㄑㄑ:經查證,是我筆誤,函數3是這樣來的
- ,請wolfram alpha幫我解,結果無解,直接打反餘切=-π/2 也無解
- 所以函數3 -π/2 < x ≤ π/2⇒(-π/2,π/2],感謝你的指正,另外函數2是不是(0,π)我不確定,如是反正切
 可能也要改了---宇帆(留言·聯絡) 2014年8月12日 (二) 07:36 (UTC)
可能也要改了---宇帆(留言·聯絡) 2014年8月12日 (二) 07:36 (UTC)
- 了解, 謝謝你的查證! --578985s(留言) 2014年8月12日 (二) 07:45 (UTC)
外部連結已修改
[編輯]各位維基人:
我剛剛修改了反餘切中的1個外部連結,請大家仔細檢查我的編輯。如果您有疑問,或者需要讓機械人忽略某個連結甚至整個頁面,請訪問這個簡單的FAQ獲取更多信息。我進行了以下修改:
- 向 http://terms.naer.edu.tw/detail/1852787/ 中加入存檔連結 https://archive.is/20140808025052/http://terms.naer.edu.tw/detail/1852787/
有關機械人修正錯誤的詳情請參閱FAQ。





![{\displaystyle \operatorname {arccot} x={\frac {i}{2}}\left[\ln \left({\frac {x-i}{x}}\right)-\ln \left({\frac {x+i}{x}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9236be612d7c5c872e9b2a46049ffafddc9c0e2)















![{\displaystyle \mathrm {Re} \left({\frac {i}{2}}\left[\ln \left({\frac {x-i}{x}}\right)-\ln \left({\frac {x+i}{x}}\right)\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59057a2fe8ab9acb197ade0454c1be11f2673e1b)
![{\displaystyle {\frac {i}{2}}\left[\ln \left({\frac {x-i}{x}}\right)-\ln \left({\frac {x+i}{x}}\right)\right]=-{\frac {\pi }{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43c174bbd36d9189406d80c08846d1d3ec00644b)