用戶:深鳴/二分搜尋演算法
| 深鳴/二分搜尋演算法 | |
|---|---|
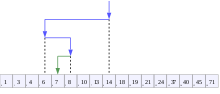 二分搜尋過程示意,目標值為7 | |
| 概況 | |
| 類別 | 搜尋演算法 |
| 資料結構 | 陣列 |
| 複雜度 | |
| 平均時間複雜度 | |
| 最壞時間複雜度 | |
| 最佳時間複雜度 | |
| 空間複雜度 | |
| 最佳解 | 是 |
| 相關變數的定義 | |
二分搜尋[2](英語:binary search,中國大陸作二分查找[1],台灣作二分搜尋[2],大陸又作二分搜索[3])[a]是用於搜尋有序陣列中目標值位置的搜尋演算法。[9][10]
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
Binary search runs in logarithmic time in the worst case, making comparisons, where is the number of elements in the array.[b][11] Binary search is faster than linear search except for small arrays. However, the array must be sorted first to be able to apply binary search. There are specialized data structures designed for fast searching, such as hash tables, that can be searched more efficiently than binary search. However, binary search can be used to solve a wider range of problems, such as finding the next-smallest or next-largest element in the array relative to the target even if it is absent from the array.
There are numerous variations of binary search. In particular, fractional cascading speeds up binary searches for the same value in multiple arrays. Fractional cascading efficiently solves a number of search problems in computational geometry and in numerous other fields. Exponential search extends binary search to unbounded lists. The binary search tree and B-tree data structures are based on binary search.
演算法
[編輯]二分搜尋適用於有序陣列。二分搜尋首先比較陣列中間的元素與目標值。如果目標值與該元素匹配,則返回該元素在陣列中的位置;如果目標值小於該元素,則在陣列較小的那一半中繼續搜尋;如果目標值大於該元素,則在陣列較大的那一半中繼續搜尋。通過這種方法,每次疊代都能將搜尋範圍縮小一半。[12]
過程
[編輯]給定一個包含個元素的陣列,其中的值或記錄分別為,且滿足。假設目標值為。下面的子程式使用二分搜尋來尋找在陣列中的索引。[12]
- 取為,為。
- 如果,則搜尋失敗並終止。
- 取(中間元素的位置)為的向下取整值,即不大於的最大整數。
- 如果,則取為,並返回步驟2。
- 如果,則取為,並返回步驟2。
- 如果,則搜尋完成,返回。
這個疊代過程使用兩個變數和來跟蹤搜尋邊界。該過程可以用偽代碼表示如下,其中變數名和類型與上文相同,floor為下取整函數,unsuccessful表示搜尋失敗時的特定返回值:[12]

function binary_search(A, n, T) is
L := 0
R := n − 1
while L ≤ R do
m := floor((L + R) / 2)
if A[m] < T then
L := m + 1
else if A[m] > T then
R := m − 1
else:
return m
return unsuccessful
也可取為的向上取整值。如此所做,若目標值在陣列中出現多次,結果可能會有所不同。
替代過程
[編輯]上述過程中,每次疊代都會檢查中間元素()是否等於目標值()。而在其他一些實現中,僅剩下一個元素(即)時,才會執行這項檢查,這樣每次疊代時就無需檢查。這種方式的比較迴圈更快,因為每次疊代少了一次比較,但平均只需要多一次疊代。[13]
赫爾曼·博滕布魯赫於1962年首次發表了省略此檢查的實現。[13][14]
- 取為,為。
- 當時,
- 取(中間元素的位置)為的向上取整值,即不小於的最小整數。
- 如果,取為。
- 否則說明,取為。
- 現在,搜尋完成。如果,返回。否則,搜尋失敗並終止。
該版本的偽代碼如下,其中ceil是上取整函數:
function binary_search_alternative(A, n, T) is
L := 0
R := n − 1
while L != R do
m := ceil((L + R) / 2)
if A[m] > T then
R := m − 1
else:
L := m
if A[L] = T then
return L
return unsuccessful
重複元素
[編輯]即使陣列中存在重複元素,演算法可能返回任意一個與目標值相等的索引。例如,如果要搜尋的陣列為,且目標值為,那麼演算法返回第4個(索引為 3)或第5個(索引為4)元素都是正確的。常規過程通常返回第4個元素(索引為3),但並不總是返回第一個重複項(考慮陣列,這時依然返回第4個元素)。然而,有時需要找到目標值在陣列中重複出現的最左側或最右側的元素。在上述例子中,第4個元素是值為4的最左側元素,而第5個元素是值為4的最右側元素。上述的替代過程總是會返回最右側元素的索引(如果該元素存在的話)。[14]
搜尋最左側元素的過程
[編輯]要搜尋最左邊的元素,可以使用以下過程:[15]
- 取為,為。
- 當時,
- 取(中間元素的位置)為的向下取整值,即不大於的最大整數。
- 如果,取為。
- 否則說明,取為。
- 返回。
如果且,那麼是等於的最左側元素。即使不在陣列中,也是在陣列中的排序位置,即陣列中小於的元素數量。
該版本的偽代碼如下,其中floor是下取整函數:
function binary_search_leftmost(A, n, T):
L := 0
R := n
while L < R:
m := floor((L + R) / 2)
if A[m] < T:
L := m + 1
else:
R := m
return L
搜尋最右側元素的過程
[編輯]要搜尋最右邊的元素,可以使用以下過程:[15]
- 取為,為。
- 當時,
- 取(中間元素的位置)為的向下取整值,即不大於的最大整數。
- 如果,取為。
- 否則說明,取為。
- 返回。
如果 且,那麼是等於的最右側元素。即使不在陣列中,也是陣列中大於的元素數量。
該版本的偽代碼如下,其中floor是下取整函數:
function binary_search_rightmost(A, n, T):
L := 0
R := n
while L < R:
m := floor((L + R) / 2)
if A[m] > T:
R := m
else:
L := m + 1
return R - 1
近似匹配
[編輯]
上述過程僅用於精確匹配,即找到目標值的位置。然而,由於二分搜尋在有序陣列上進行,所以很容易擴充它以執行近似匹配。例如,二分搜尋可以用來計算給定值的排序位置(即比它小的元素的數量)、前驅(前一個較小的元素)、後繼(下一個較大的元素)、最近鄰。範圍查詢(搜尋兩個值之間的元素數量)可以通過查詢兩次排序位置來完成。[16]
- 查詢排序位置可以使用搜尋最左側元素的過程來完成。程式的返回值即為小於目標值的元素數量。[16]
- 查詢前驅可以通過查詢排序位置來執行。如果目標值的排序位置為,那麼其前驅的位置為。[17]
- 對於後繼查詢,可以搜尋最右側元素。如果得到的結果為,那麼目標值的後繼位置就是。[17]
- 目標值的最近鄰是其前驅或後繼之一,取決於哪個位置更接近。
- 區間查詢也很簡單。[17]一旦知道了兩個值的位置,區間內大於等於第一個值且小於第二個值的元素數量就是兩個位置之差。考慮到是否需要將區間的端點包含在內,以及陣列中是否包含與端點匹配的元素,其結果可能會增加或減少1。[18]
效能
[編輯]

就比較次數而言,可以將二分搜尋的過程放在二叉樹上執行,以分析其效能。樹的根節點是陣列的中間元素。左半部分的中間元素是根節點的左子節點,右半部分的中間元素是根節點的右子節點,其餘部分以類似方式構建。搜尋過程從根節點開始,根據目標值是小於還是大於當前節點的值來選擇遍歷左子樹還是右子樹。[11][19]
最壞情況下,二分搜尋需要比較次。此時搜尋會達到樹的最深層,並且對於任何二分搜尋,樹的層數總為。若目標元素不在陣列中,可能會發生最壞情況:若可以表示為2的某次冪減1,那麼搜尋過程總會遍歷到最深層,一定會發生最壞情況;否則,搜尋過程可能會在倒數第二層中止,此時比較了次,比最壞情況少一次。[20]
平均情況下,當目標元素在陣列中時,二分搜尋的比較次數是(假設每個元素被搜尋的概率相等),近似於;若目標元素不在陣列中,二分搜尋的比較次數平均為(假設範圍內及範圍外的元素被搜尋的概率相等)。[19]
最好情況下,即目標值正好是陣列的中間元素,二分搜尋在一次比較後就能返回其位置。[21]
In terms of iterations, no search algorithm that works only by comparing elements can exhibit better average and worst-case performance than binary search. The comparison tree representing binary search has the fewest levels possible as every level above the lowest level of the tree is filled completely.[c] Otherwise, the search algorithm can eliminate few elements in an iteration, increasing the number of iterations required in the average and worst case. This is the case for other search algorithms based on comparisons, as while they may work faster on some target values, the average performance over all elements is worse than binary search. By dividing the array in half, binary search ensures that the size of both subarrays are as similar as possible.[19]
空間複雜度
[編輯]Binary search requires three pointers to elements, which may be array indices or pointers to memory locations, regardless of the size of the array. Therefore, the space complexity of binary search is in the word RAM model of computation.
平均情況的推導
[編輯]The average number of iterations performed by binary search depends on the probability of each element being searched. The average case is different for successful searches and unsuccessful searches. It will be assumed that each element is equally likely to be searched for successful searches. For unsuccessful searches, it will be assumed that the intervals between and outside elements are equally likely to be searched. The average case for successful searches is the number of iterations required to search every element exactly once, divided by , the number of elements. The average case for unsuccessful searches is the number of iterations required to search an element within every interval exactly once, divided by the intervals.[19]
成功的搜尋
[編輯]In the binary tree representation, a successful search can be represented by a path from the root to the target node, called an internal path. The length of a path is the number of edges (connections between nodes) that the path passes through. The number of iterations performed by a search, given that the corresponding path has length , is counting the initial iteration. The internal path length is the sum of the lengths of all unique internal paths. Since there is only one path from the root to any single node, each internal path represents a search for a specific element. If there are elements, which is a positive integer, and the internal path length is , then the average number of iterations for a successful search , with the one iteration added to count the initial iteration.[19]
Since binary search is the optimal algorithm for searching with comparisons, this problem is reduced to calculating the minimum internal path length of all binary trees with nodes, which is equal to:[22]
For example, in a 7-element array, the root requires one iteration, the two elements below the root require two iterations, and the four elements below require three iterations. In this case, the internal path length is:[22]
The average number of iterations would be based on the equation for the average case. The sum for can be simplified to:[19]
Substituting the equation for into the equation for :[19]
For integer , this is equivalent to the equation for the average case on a successful search specified above.
失敗的搜尋
[編輯]Unsuccessful searches can be represented by augmenting the tree with external nodes, which forms an extended binary tree. If an internal node, or a node present in the tree, has fewer than two child nodes, then additional child nodes, called external nodes, are added so that each internal node has two children. By doing so, an unsuccessful search can be represented as a path to an external node, whose parent is the single element that remains during the last iteration. An external path is a path from the root to an external node. The external path length is the sum of the lengths of all unique external paths. If there are elements, which is a positive integer, and the external path length is , then the average number of iterations for an unsuccessful search , with the one iteration added to count the initial iteration. The external path length is divided by instead of because there are external paths, representing the intervals between and outside the elements of the array.[19]
This problem can similarly be reduced to determining the minimum external path length of all binary trees with nodes. For all binary trees, the external path length is equal to the internal path length plus .[22] Substituting the equation for :[19]
Substituting the equation for into the equation for , the average case for unsuccessful searches can be determined:[19]
另一過程的效能
[編輯]Each iteration of the binary search procedure defined above makes one or two comparisons, checking if the middle element is equal to the target in each iteration. Assuming that each element is equally likely to be searched, each iteration makes 1.5 comparisons on average. A variation of the algorithm checks whether the middle element is equal to the target at the end of the search. On average, this eliminates half a comparison from each iteration. This slightly cuts the time taken per iteration on most computers. However, it guarantees that the search takes the maximum number of iterations, on average adding one iteration to the search. Because the comparison loop is performed only times in the worst case, the slight increase in efficiency per iteration does not compensate for the extra iteration for all but very large .[d][23][24]
執行時間和快取使用
[編輯]In analyzing the performance of binary search, another consideration is the time required to compare two elements. For integers and strings, the time required increases linearly as the encoding length (usually the number of bits) of the elements increase. For example, comparing a pair of 64-bit unsigned integers would require comparing up to double the bits as comparing a pair of 32-bit unsigned integers. The worst case is achieved when the integers are equal. This can be significant when the encoding lengths of the elements are large, such as with large integer types or long strings, which makes comparing elements expensive. Furthermore, comparing floating-point values (the most common digital representation of real numbers) is often more expensive than comparing integers or short strings.[25]
On most computer architectures, the processor has a hardware cache separate from RAM. Since they are located within the processor itself, caches are much faster to access but usually store much less data than RAM. Therefore, most processors store memory locations that have been accessed recently, along with memory locations close to it. For example, when an array element is accessed, the element itself may be stored along with the elements that are stored close to it in RAM, making it faster to sequentially access array elements that are close in index to each other (locality of reference). On a sorted array, binary search can jump to distant memory locations if the array is large, unlike algorithms (such as linear search and linear probing in hash tables) which access elements in sequence. This adds slightly to the running time of binary search for large arrays on most systems.[25]
二分搜尋與其他方案
[編輯]Sorted arrays with binary search are a very inefficient solution when insertion and deletion operations are interleaved with retrieval, taking time for each such operation. In addition, sorted arrays can complicate memory use especially when elements are often inserted into the array.[26] There are other data structures that support much more efficient insertion and deletion. Binary search can be used to perform exact matching and set membership (determining whether a target value is in a collection of values). There are data structures that support faster exact matching and set membership. However, unlike many other searching schemes, binary search can be used for efficient approximate matching, usually performing such matches in time regardless of the type or structure of the values themselves.[27] In addition, there are some operations, like finding the smallest and largest element, that can be performed efficiently on a sorted array.[16]
線性搜尋
[編輯]Linear search is a simple search algorithm that checks every record until it finds the target value. Linear search can be done on a linked list, which allows for faster insertion and deletion than an array. Binary search is faster than linear search for sorted arrays except if the array is short, although the array needs to be sorted beforehand.[e][29] All sorting algorithms based on comparing elements, such as quicksort and merge sort, require at least comparisons in the worst case.[30] Unlike linear search, binary search can be used for efficient approximate matching. There are operations such as finding the smallest and largest element that can be done efficiently on a sorted array but not on an unsorted array.[31]
二叉樹
[編輯]
A binary search tree is a binary tree data structure that works based on the principle of binary search. The records of the tree are arranged in sorted order, and each record in the tree can be searched using an algorithm similar to binary search, taking on average logarithmic time. Insertion and deletion also require on average logarithmic time in binary search trees. This can be faster than the linear time insertion and deletion of sorted arrays, and binary trees retain the ability to perform all the operations possible on a sorted array, including range and approximate queries.[27][32]
However, binary search is usually more efficient for searching as binary search trees will most likely be imperfectly balanced, resulting in slightly worse performance than binary search. This even applies to balanced binary search trees, binary search trees that balance their own nodes, because they rarely produce the tree with the fewest possible levels. Except for balanced binary search trees, the tree may be severely imbalanced with few internal nodes with two children, resulting in the average and worst-case search time approaching comparisons.[f] Binary search trees take more space than sorted arrays.[34]
Binary search trees lend themselves to fast searching in external memory stored in hard disks, as binary search trees can be efficiently structured in filesystems. The B-tree generalizes this method of tree organization. B-trees are frequently used to organize long-term storage such as databases and filesystems.[35][36]
雜湊表
[編輯]For implementing associative arrays, hash tables, a data structure that maps keys to records using a hash function, are generally faster than binary search on a sorted array of records.[37] Most hash table implementations require only amortized constant time on average.[g][39] However, hashing is not useful for approximate matches, such as computing the next-smallest, next-largest, and nearest key, as the only information given on a failed search is that the target is not present in any record.[40] Binary search is ideal for such matches, performing them in logarithmic time. Binary search also supports approximate matches. Some operations, like finding the smallest and largest element, can be done efficiently on sorted arrays but not on hash tables.[27]
集合
[編輯]A related problem to search is set membership. Any algorithm that does lookup, like binary search, can also be used for set membership. There are other algorithms that are more specifically suited for set membership. A bit array is the simplest, useful when the range of keys is limited. It compactly stores a collection of bits, with each bit representing a single key within the range of keys. Bit arrays are very fast, requiring only time.[41] The Judy1 type of Judy array handles 64-bit keys efficiently.[42]
For approximate results, Bloom filters, another probabilistic data structure based on hashing, store a set of keys by encoding the keys using a bit array and multiple hash functions. Bloom filters are much more space-efficient than bit arrays in most cases and not much slower: with hash functions, membership queries require only time. However, Bloom filters suffer from false positives.[h][i][44]
其他數據結構
[編輯]There exist data structures that may improve on binary search in some cases for both searching and other operations available for sorted arrays. For example, searches, approximate matches, and the operations available to sorted arrays can be performed more efficiently than binary search on specialized data structures such as van Emde Boas trees, fusion trees, tries, and bit arrays. These specialized data structures are usually only faster because they take advantage of the properties of keys with a certain attribute (usually keys that are small integers), and thus will be time or space consuming for keys that lack that attribute.[27] As long as the keys can be ordered, these operations can always be done at least efficiently on a sorted array regardless of the keys. Some structures, such as Judy arrays, use a combination of approaches to mitigate this while retaining efficiency and the ability to perform approximate matching.[42]
其他形式
[編輯]統一二分搜尋
[編輯]
Uniform binary search stores, instead of the lower and upper bounds, the difference in the index of the middle element from the current iteration to the next iteration. A lookup table containing the differences is computed beforehand. For example, if the array to be searched is [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], the middle element () would be 6. In this case, the middle element of the left subarray ([1, 2, 3, 4, 5]) is 3 and the middle element of the right subarray ([7, 8, 9, 10, 11]) is 9. Uniform binary search would store the value of 3 as both indices differ from 6 by this same amount.[45] To reduce the search space, the algorithm either adds or subtracts this change from the index of the middle element. Uniform binary search may be faster on systems where it is inefficient to calculate the midpoint, such as on decimal computers.[46]
指數搜尋
[編輯]
Exponential search extends binary search to unbounded lists. It starts by finding the first element with an index that is both a power of two and greater than the target value. Afterwards, it sets that index as the upper bound, and switches to binary search. A search takes iterations before binary search is started and at most iterations of the binary search, where is the position of the target value. Exponential search works on bounded lists, but becomes an improvement over binary search only if the target value lies near the beginning of the array.[47]
插值搜尋
[編輯]
Instead of calculating the midpoint, interpolation search estimates the position of the target value, taking into account the lowest and highest elements in the array as well as length of the array. It works on the basis that the midpoint is not the best guess in many cases. For example, if the target value is close to the highest element in the array, it is likely to be located near the end of the array.[48]
A common interpolation function is linear interpolation. If is the array, are the lower and upper bounds respectively, and is the target, then the target is estimated to be about of the way between and . When linear interpolation is used, and the distribution of the array elements is uniform or near uniform, interpolation search makes comparisons.[48][49][50]
In practice, interpolation search is slower than binary search for small arrays, as interpolation search requires extra computation. Its time complexity grows more slowly than binary search, but this only compensates for the extra computation for large arrays.[48]
分數級聯
[編輯]
Fractional cascading is a technique that speeds up binary searches for the same element in multiple sorted arrays. Searching each array separately requires time, where is the number of arrays. Fractional cascading reduces this to by storing specific information in each array about each element and its position in the other arrays.[51][52]
Fractional cascading was originally developed to efficiently solve various computational geometry problems. Fractional cascading has been applied elsewhere, such as in data mining and Internet Protocol routing.[51]
推廣到圖表
[編輯]Binary search has been generalized to work on certain types of graphs, where the target value is stored in a vertex instead of an array element. Binary search trees are one such generalization—when a vertex (node) in the tree is queried, the algorithm either learns that the vertex is the target, or otherwise which subtree the target would be located in. However, this can be further generalized as follows: given an undirected, positively weighted graph and a target vertex, the algorithm learns upon querying a vertex that it is equal to the target, or it is given an incident edge that is on the shortest path from the queried vertex to the target. The standard binary search algorithm is simply the case where the graph is a path. Similarly, binary search trees are the case where the edges to the left or right subtrees are given when the queried vertex is unequal to the target. For all undirected, positively weighted graphs, there is an algorithm that finds the target vertex in queries in the worst case.[53]
嘈雜二分搜尋
[編輯]
Noisy binary search algorithms solve the case where the algorithm cannot reliably compare elements of the array. For each pair of elements, there is a certain probability that the algorithm makes the wrong comparison. Noisy binary search can find the correct position of the target with a given probability that controls the reliability of the yielded position. Every noisy binary search procedure must make at least comparisons on average, where is the binary entropy function and is the probability that the procedure yields the wrong position.[54][55][56] The noisy binary search problem can be considered as a case of the Rényi-Ulam game,[57] a variant of Twenty Questions where the answers may be wrong.[58]
量子二分搜尋
[編輯]Classical computers are bounded to the worst case of exactly iterations when performing binary search. Quantum algorithms for binary search are still bounded to a proportion of queries (representing iterations of the classical procedure), but the constant factor is less than one, providing for a lower time complexity on quantum computers. Any exact quantum binary search procedure—that is, a procedure that always yields the correct result—requires at least queries in the worst case, where is the natural logarithm.[59] There is an exact quantum binary search procedure that runs in queries in the worst case.[60] In comparison, Grover's algorithm is the optimal quantum algorithm for searching an unordered list of elements, and it requires queries.[61]
歷史
[編輯]The idea of sorting a list of items to allow for faster searching dates back to antiquity. The earliest known example was the Inakibit-Anu tablet from Babylon dating back to 約200 BCE. The tablet contained about 500 sexagesimal numbers and their reciprocals sorted in lexicographical order, which made searching for a specific entry easier. In addition, several lists of names that were sorted by their first letter were discovered on the Aegean Islands. Catholicon, a Latin dictionary finished in 1286 CE, was the first work to describe rules for sorting words into alphabetical order, as opposed to just the first few letters.[14]
In 1946, John Mauchly made the first mention of binary search as part of the Moore School Lectures, a seminal and foundational college course in computing.[14] In 1957, William Wesley Peterson published the first method for interpolation search.[14][62] Every published binary search algorithm worked only for arrays whose length is one less than a power of two[j] until 1960, when Derrick Henry Lehmer published a binary search algorithm that worked on all arrays.[64] In 1962, Hermann Bottenbruch presented an ALGOL 60 implementation of binary search that placed the comparison for equality at the end, increasing the average number of iterations by one, but reducing to one the number of comparisons per iteration.[13] The uniform binary search was developed by A. K. Chandra of Stanford University in 1971.[14] In 1986, Bernard Chazelle and Leonidas J. Guibas introduced fractional cascading as a method to solve numerous search problems in computational geometry.[51][65][66]
實現問題
[編輯]儘管二分搜尋的基本思想相對簡單,但其細節卻出奇複雜。
喬恩·本特利在為職業程式設計師開設的一門課程中佈置了二分搜尋的練習,發現90%的學生在數小時後仍未能給出正確的解答。主要原因是演算法實現有誤而無法執行,或是在極少數邊界情況下返回錯誤答案。[67]1988年發表的一項研究顯示,二十本教材中只有五本給出了準確的二分搜尋代碼。[68]此外,本特利自身在1986年出版的《編程珠璣》一書中給出的二分搜尋實現存在溢位錯誤,這個錯誤在二十多年裏未被發現。Java程式語言庫中的二分搜尋實現也存在相同的溢位問題,且該問題持續了九年多。[69]
在實際編程中,表示索引的變數通常是固定大小的(整數)。因此在處理非常大的陣列時,可能會導致算術溢位。如果使用計算中點,即使和的值都在所用資料類型的表示範圍內,的值仍可能會超過範圍。如果和都是非負數,可以通過計算來避免這種情況。[70]
如果迴圈的退出條件定義不正確,可能會導致無限迴圈。當超過時,表示搜尋失敗,必須返回失敗的資訊。另外,迴圈應在找到目標元素時退出;若不這麼做,那麼在迴圈結束後,必須檢查是否成功找到目標元素。本特利發現,大多數在實現二分搜尋時出錯的程式設計師,都是在定義退出條件時犯了錯。[13][71]
庫支援
[編輯]許多程式語言的標準庫包含二分搜尋常式:
- C語言在其標準庫中提供了
bsearch()函數,通常使用二分搜尋實現,儘管官方標準中並未強制要求。[72] - C++的標準庫中提供了
binary_search()、lower_bound()、upper_bound()、equal_range()函數。[73] - D語言的標準庫Phobos在
std.range模組中提供了SortedRange類型(由sort()和assumeSorted()函數返回),該類型包含contains()、equaleRange()、lowerBound()、trisect()方法,這些方法預設對提供隨機訪問的範圍使用二分搜尋技術。[74] - COBOL提供了
SEARCH ALL動詞,用於對COBOL有序表執行二分搜尋。[75] - Go的
sort標準庫包包含Search、SearchInts、SearchFloat64s、SearchStrings函數,分別實現了通用的二分搜尋,以及針對整數、浮點數、字串切片的特定實現。[76] - Java在標準
java.util包的Arrays和Collections類中提供了一組多載的binarySearch()靜態方法,用於對Java陣列和List(列表)執行二分搜尋。[77][78] - Microsoft的.NET Framework 2.0在其集合基礎類別中提供了二分搜尋演算法的靜態泛型版本,例如
System.Array的BinarySearch<T>(T[] array, T value)方法。[79] - 對於Objective-C,Cocoa框架在Mac OS X 10.6及以上版本中提供了
NSArray -indexOfObject:inSortedRange:options:usingComparator:方法;[80]蘋果的Core Foundation C框架也包含CFArrayBSearchValues()函數。[81] - Python提供了模組
bisect,在插入元素後仍能保持列表的有序狀態,而無需每次插入元素後都對列表排序。[82] - Ruby的Array類包含一個帶有內建近似匹配的
bsearch方法。[83] - Rust的切片原始類型提供了
binary_search()、binary_search_by()、binary_search_by_key()、partition_point()方法。[84]
參見
[編輯]- Bisection method – the same idea used to solve equations in the real numbers
- Multiplicative binary search
註釋和參考文獻
[編輯]註釋
[編輯]- ^ 又稱折半搜尋(英語:half-interval search[5],中國大陸作折半查找[4],台灣作折半搜尋,大陸又作折半搜索[6],直譯為「半區間搜尋」)、對數搜尋(英語:logarithmic search[7]),英文中又稱binary chop[8](chop有「劈、斬」之意)。
- ^ The is Big O notation, and is the logarithm. In Big O notation, the base of the logarithm does not matter since every logarithm of a given base is a constant factor of another logarithm of another base. That is, , where is a constant.
- ^ Any search algorithm based solely on comparisons can be represented using a binary comparison tree. An internal path is any path from the root to an existing node. Let be the internal path length, the sum of the lengths of all internal paths. If each element is equally likely to be searched, the average case is or simply one plus the average of all the internal path lengths of the tree. This is because internal paths represent the elements that the search algorithm compares to the target. The lengths of these internal paths represent the number of iterations after the root node. Adding the average of these lengths to the one iteration at the root yields the average case. Therefore, to minimize the average number of comparisons, the internal path length must be minimized. It turns out that the tree for binary search minimizes the internal path length. Knuth 1998 proved that the external path length (the path length over all nodes where both children are present for each already-existing node) is minimized when the external nodes (the nodes with no children) lie within two consecutive levels of the tree. This also applies to internal paths as internal path length is linearly related to external path length . For any tree of nodes, . When each subtree has a similar number of nodes, or equivalently the array is divided into halves in each iteration, the external nodes as well as their interior parent nodes lie within two levels. It follows that binary search minimizes the number of average comparisons as its comparison tree has the lowest possible internal path length.[19]
- ^ Knuth 1998 showed on his MIX computer model, which Knuth designed as a representation of an ordinary computer, that the average running time of this variation for a successful search is units of time compared to units for regular binary search. The time complexity for this variation grows slightly more slowly, but at the cost of higher initial complexity. [23]
- ^ Knuth 1998 performed a formal time performance analysis of both of these search algorithms. On Knuth's MIX computer, which Knuth designed as a representation of an ordinary computer, binary search takes on average units of time for a successful search, while linear search with a sentinel node at the end of the list takes units. Linear search has lower initial complexity because it requires minimal computation, but it quickly outgrows binary search in complexity. On the MIX computer, binary search only outperforms linear search with a sentinel if .[19][28]
- ^ Inserting the values in sorted order or in an alternating lowest-highest key pattern will result in a binary search tree that maximizes the average and worst-case search time.[33]
- ^ It is possible to search some hash table implementations in guaranteed constant time.[38]
- ^ This is because simply setting all of the bits which the hash functions point to for a specific key can affect queries for other keys which have a common hash location for one or more of the functions.[43]
- ^ There exist improvements of the Bloom filter which improve on its complexity or support deletion; for example, the cuckoo filter exploits cuckoo hashing to gain these advantages.[43]
- ^ That is, arrays of length 1, 3, 7, 15, 31 ...[63]
參照
[編輯]- ^ Sedgewick, Wayne & 謝路雲 2012,§3.1.5 有序陣列中的二分搜尋.
- ^ 廖永申; 王欣平. 在嵌入式Linux系統上的新一代網路協定轉換軟體開發. 2003年NCS全國計算機會議. 2006-06-12 [2024-07-16] (中文(臺灣)).
- ^ 韋純福. 基于分治思想的二分搜索技术研究. 大眾科技. 2008, (3): 58–59. CNKI DZJI200803022
 (中文(中國大陸)).
(中文(中國大陸)).
- ^ 駱劍鋒. 哈希表与一般查找方法的比较及冲突的解决. 十堰職業技術學院學報. 2007, (5): 96–98. CNKI SYZJ200705034
 (中文(中國大陸)).
(中文(中國大陸)).
- ^ Williams, Jr., Louis F. A modification to the half-interval search (binary search) method. Proceedings of the 14th ACM Southeast Conference. ACM: 95–101. 1976-04-22. doi:10.1145/503561.503582
 .
.
- ^ 王曉東. 一种在TQuery记录集中实现快速搜索的方法. 管理資訊系統. 2000, (3): 56–57. CNKI JYXX200003023
 (中文(中國大陸)).
(中文(中國大陸)).
- ^ 7.0 7.1 Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "Binary search".
- ^ Butterfield & Ngondi 2016,第46頁.
- ^ Cormen et al. 2009,第39頁.
- ^ 埃里克·韋斯坦因. Binary search. MathWorld.
- ^ 11.0 11.1 Flores, Ivan; Madpis, George. Average binary search length for dense ordered lists. Communications of the ACM. 1971-09-01, 14 (9): 602–603. ISSN 0001-0782. S2CID 43325465. doi:10.1145/362663.362752
 .
.
- ^ 12.0 12.1 12.2 Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "Algorithm B".
- ^ 13.0 13.1 13.2 13.3 Bottenbruch, Hermann. Structure and use of ALGOL 60. Journal of the ACM. 1962-04-01, 9 (2): 161–221. ISSN 0004-5411. S2CID 13406983. doi:10.1145/321119.321120
 . Procedure is described at p. 214 (§43), titled "Program for Binary Search".
. Procedure is described at p. 214 (§43), titled "Program for Binary Search".
- ^ 14.0 14.1 14.2 14.3 14.4 14.5 Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "History and bibliography".
- ^ 15.0 15.1 Kasahara & Morishita 2006,第8–9頁.
- ^ 16.0 16.1 16.2 Sedgewick & Wayne 2011,§3.1, subsection "Rank and selection".
- ^ 17.0 17.1 17.2 Goldman & Goldman 2008,第461–463頁.
- ^ Sedgewick & Wayne 2011,§3.1, subsection "Range queries".
- ^ 19.00 19.01 19.02 19.03 19.04 19.05 19.06 19.07 19.08 19.09 19.10 19.11 Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "Further analysis of binary search".
- ^ Knuth 1998,§6.2.1 ("Searching an ordered table"), "Theorem B".
- ^ Chang 2003,第169頁.
- ^ 22.0 22.1 22.2 Knuth 1997,§2.3.4.5 ("Path length").
- ^ 23.0 23.1 Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "Exercise 23".
- ^ Rolfe, Timothy J. Analytic derivation of comparisons in binary search. ACM SIGNUM Newsletter. 1997, 32 (4): 15–19. S2CID 23752485. doi:10.1145/289251.289255
 .
.
- ^ 25.0 25.1 Khuong, Paul-Virak; Morin, Pat. Array Layouts for Comparison-Based Searching. Journal of Experimental Algorithmics. 2017, 22. Article 1.3. S2CID 23752485. arXiv:1509.05053
 . doi:10.1145/3053370.
. doi:10.1145/3053370.
- ^ Knuth 1997,§2.2.2 ("Sequential Allocation").
- ^ 27.0 27.1 27.2 27.3 Beame, Paul; Fich, Faith E. Optimal bounds for the predecessor problem and related problems. Journal of Computer and System Sciences. 2001, 65 (1): 38–72. doi:10.1006/jcss.2002.1822
 .
.
- ^ Knuth 1998,Answers to Exercises (§6.2.1) for "Exercise 5".
- ^ Knuth 1998,§6.2.1 ("Searching an ordered table").
- ^ Knuth 1998,§5.3.1 ("Minimum-Comparison sorting").
- ^ Sedgewick & Wayne 2011,§3.2 ("Ordered symbol tables").
- ^ Sedgewick & Wayne 2011,§3.2 ("Binary Search Trees"), subsection "Order-based methods and deletion".
- ^ Knuth 1998,§6.2.2 ("Binary tree searching"), subsection "But what about the worst case?".
- ^ Sedgewick & Wayne 2011,§3.5 ("Applications"), "Which symbol-table implementation should I use?".
- ^ Knuth 1998,§5.4.9 ("Disks and Drums").
- ^ Knuth 1998,§6.2.4 ("Multiway trees").
- ^ Knuth 1998,§6.4 ("Hashing").
- ^ Knuth 1998,§6.4 ("Hashing"), subsection "History".
- ^ Dietzfelbinger, Martin; Karlin, Anna; Mehlhorn, Kurt; Meyer auf der Heide, Friedhelm; Rohnert, Hans; Tarjan, Robert E. Dynamic perfect hashing: upper and lower bounds. SIAM Journal on Computing. August 1994, 23 (4): 738–761. doi:10.1137/S0097539791194094.
- ^ Morin, Pat. Hash tables (PDF): 1. [2016-03-28]. (原始內容存檔 (PDF)於2022-10-09).
- ^ Knuth 2011,§7.1.3 ("Bitwise Tricks and Techniques").
- ^ 42.0 42.1 Silverstein, Alan, Judy IV shop manual (PDF), Hewlett-Packard: 80–81, (原始內容存檔 (PDF)於2022-10-09)
- ^ 43.0 43.1 Fan, Bin; Andersen, Dave G.; Kaminsky, Michael; Mitzenmacher, Michael D. Cuckoo filter: practically better than Bloom. Proceedings of the 10th ACM International on Conference on Emerging Networking Experiments and Technologies: 75–88. 2014. doi:10.1145/2674005.2674994
 .
.
- ^ Bloom, Burton H. Space/time trade-offs in hash coding with allowable errors. Communications of the ACM. 1970, 13 (7): 422–426. CiteSeerX 10.1.1.641.9096
 . S2CID 7931252. doi:10.1145/362686.362692.
. S2CID 7931252. doi:10.1145/362686.362692.
- ^ Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "An important variation".
- ^ Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "Algorithm U".
- ^ Moffat & Turpin 2002,第33頁.
- ^ 48.0 48.1 48.2 Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "Interpolation search".
- ^ Knuth 1998,§6.2.1 ("Searching an ordered table"), subsection "Exercise 22".
- ^ Perl, Yehoshua; Itai, Alon; Avni, Haim. Interpolation search—a log log n search. Communications of the ACM. 1978, 21 (7): 550–553. S2CID 11089655. doi:10.1145/359545.359557
 .
.
- ^ 51.0 51.1 51.2 Chazelle, Bernard; Liu, Ding. Lower bounds for intersection searching and fractional cascading in higher dimension. 33rd ACM Symposium on Theory of Computing. ACM: 322–329. 2001-07-06 [2018-06-30]. ISBN 978-1-58113-349-3. doi:10.1145/380752.380818.
- ^ Chazelle, Bernard; Liu, Ding. Lower bounds for intersection searching and fractional cascading in higher dimension (PDF). Journal of Computer and System Sciences. 2004-03-01, 68 (2): 269–284 [2018-06-30]. CiteSeerX 10.1.1.298.7772
 . ISSN 0022-0000. doi:10.1016/j.jcss.2003.07.003. (原始內容存檔 (PDF)於2022-10-09) (英語).
. ISSN 0022-0000. doi:10.1016/j.jcss.2003.07.003. (原始內容存檔 (PDF)於2022-10-09) (英語).
- ^ Emamjomeh-Zadeh, Ehsan; Kempe, David; Singhal, Vikrant. Deterministic and probabilistic binary search in graphs. 48th ACM Symposium on Theory of Computing: 519–532. 2016. arXiv:1503.00805
 . doi:10.1145/2897518.2897656.
. doi:10.1145/2897518.2897656.
- ^ Ben-Or, Michael; Hassidim, Avinatan. The Bayesian learner is optimal for noisy binary search (and pretty good for quantum as well) (PDF). 49th Symposium on Foundations of Computer Science: 221–230. 2008. ISBN 978-0-7695-3436-7. doi:10.1109/FOCS.2008.58. (原始內容存檔 (PDF)於2022-10-09).
- ^ Pelc, Andrzej. Searching with known error probability. Theoretical Computer Science. 1989, 63 (2): 185–202. doi:10.1016/0304-3975(89)90077-7
 .
.
- ^ Rivest, Ronald L.; Meyer, Albert R.; Kleitman, Daniel J.; Winklmann, K. Coping with errors in binary search procedures. 10th ACM Symposium on Theory of Computing. doi:10.1145/800133.804351
 .
.
- ^ Pelc, Andrzej. Searching games with errors—fifty years of coping with liars. Theoretical Computer Science. 2002, 270 (1–2): 71–109. doi:10.1016/S0304-3975(01)00303-6
 .
.
- ^ Rényi, Alfréd. On a problem in information theory. Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei. 1961, 6: 505–516. MR 0143666 (匈牙利語).
- ^ Høyer, Peter; Neerbek, Jan; Shi, Yaoyun. Quantum complexities of ordered searching, sorting, and element distinctness. Algorithmica. 2002, 34 (4): 429–448. S2CID 13717616. arXiv:quant-ph/0102078
 . doi:10.1007/s00453-002-0976-3.
. doi:10.1007/s00453-002-0976-3.
- ^ Childs, Andrew M.; Landahl, Andrew J.; Parrilo, Pablo A. Quantum algorithms for the ordered search problem via semidefinite programming. Physical Review A. 2007, 75 (3). 032335. Bibcode:2007PhRvA..75c2335C. S2CID 41539957. arXiv:quant-ph/0608161
 . doi:10.1103/PhysRevA.75.032335.
. doi:10.1103/PhysRevA.75.032335.
- ^ Grover, Lov K. A fast quantum mechanical algorithm for database search. 28th ACM Symposium on Theory of Computing. Philadelphia, PA: 212–219. 1996. arXiv:quant-ph/9605043
 . doi:10.1145/237814.237866.
. doi:10.1145/237814.237866.
- ^ Peterson, William Wesley. Addressing for random-access storage. IBM Journal of Research and Development. 1957, 1 (2): 130–146. doi:10.1147/rd.12.0130.
- ^ "2n−1". OEIS A000225 互聯網檔案館的存檔,存檔日期2016-06-08.. Retrieved 7 May 2016.
- ^ Lehmer, Derrick. Teaching combinatorial tricks to a computer. Proceedings of Symposia in Applied Mathematics. 1960, 10: 180–181. ISBN 9780821813102. doi:10.1090/psapm/010
 .
.
- ^ Chazelle, Bernard; Guibas, Leonidas J. Fractional cascading: I. A data structuring technique (PDF). Algorithmica. 1986, 1 (1–4): 133–162. CiteSeerX 10.1.1.117.8349
 . S2CID 12745042. doi:10.1007/BF01840440.
. S2CID 12745042. doi:10.1007/BF01840440.
- ^ Chazelle, Bernard; Guibas, Leonidas J., Fractional cascading: II. Applications (PDF), Algorithmica, 1986, 1 (1–4): 163–191, S2CID 11232235, doi:10.1007/BF01840441
- ^ Bentley 2000,§4.1 ("The Challenge of Binary Search").
- ^ Pattis, Richard E. Textbook errors in binary searching. SIGCSE Bulletin. 1988, 20: 190–194. doi:10.1145/52965.53012.
- ^ Bloch, Joshua. Extra, extra – read all about it: nearly all binary searches and mergesorts are broken. Google Research Blog. 2006-06-02 [2016-04-21]. (原始內容存檔於2016-04-01).
- ^ Ruggieri, Salvatore. On computing the semi-sum of two integers (PDF). Information Processing Letters. 2003, 87 (2): 67–71 [2016-03-19]. CiteSeerX 10.1.1.13.5631
 . doi:10.1016/S0020-0190(03)00263-1. (原始內容存檔 (PDF)於2006-07-03).
. doi:10.1016/S0020-0190(03)00263-1. (原始內容存檔 (PDF)於2006-07-03).
- ^ Bentley 2000,§4.4 ("Principles").
- ^ bsearch – binary search a sorted table. The Open Group Base Specifications 7th. The Open Group. 2013 [2016-03-28]. (原始內容存檔於2016-03-21).
- ^ Stroustrup 2013,第945頁.
- ^ std.range - D Programming Language. dlang.org. [2020-04-29].
- ^ Unisys, COBOL ANSI-85 programming reference manual 1: 598–601, 2012
- ^ Package sort. The Go Programming Language. [2016-04-28]. (原始內容存檔於2016-04-25).
- ^ java.util.Arrays. Java Platform Standard Edition 8 Documentation. Oracle Corporation. [2016-05-01]. (原始內容存檔於2016-04-29).
- ^ java.util.Collections. Java Platform Standard Edition 8 Documentation. Oracle Corporation. [2016-05-01]. (原始內容存檔於2016-04-23).
- ^ List<T>.BinarySearch method (T). Microsoft Developer Network. [2016-04-10]. (原始內容存檔於2016-05-07).
- ^ NSArray. Mac Developer Library. Apple Inc. [2016-05-01]. (原始內容存檔於2016-04-17).
- ^ CFArray. Mac Developer Library. Apple Inc. [2016-05-01]. (原始內容存檔於2016-04-20).
- ^ 8.6. bisect — Array bisection algorithm. The Python Standard Library. Python Software Foundation. [2018-03-26]. (原始內容存檔於2018-03-25).
- ^ Fitzgerald 2015,第152頁.
- ^ Primitive Type
slice. The Rust Standard Library. The Rust Foundation. 2024 [2024-05-25].
來源
[編輯]- Bentley, Jon. Programming pearls 2nd. Addison-Wesley. 2000. ISBN 978-0-201-65788-3 (英語).
- Butterfield, Andrew; Ngondi, Gerard E. A dictionary of computer science 7th. Oxford, UK: Oxford University Press. 2016. ISBN 978-0-19-968897-5 (英語).
- Chang, Shi-Kuo. Data structures and algorithms. Software Engineering and Knowledge Engineering 13. Singapore: World Scientific. 2003. ISBN 978-981-238-348-8 (英語).
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. Introduction to algorithms 3rd. MIT Press and McGraw-Hill. 2009. ISBN 978-0-262-03384-8 (英語).
- Fitzgerald, Michael. Ruby pocket reference. Sebastopol, California: O'Reilly Media. 2015. ISBN 978-1-4919-2601-7 (英語).
- Goldman, Sally A.; Goldman, Kenneth J. A practical guide to data structures and algorithms using Java. Boca Raton, Florida: CRC Press. 2008. ISBN 978-1-58488-455-2 (英語).
- Kasahara, Masahiro; Morishita, Shinichi. Large-scale genome sequence processing. London, UK: Imperial College Press. 2006. ISBN 978-1-86094-635-6 (英語).
- Knuth, Donald. Fundamental algorithms. The Art of Computer Programming 1 3rd. Reading, MA: Addison-Wesley Professional. 1997. ISBN 978-0-201-89683-1 (英語).
- Knuth, Donald. Sorting and searching. The Art of Computer Programming 3 2nd. Reading, MA: Addison-Wesley Professional. 1998. ISBN 978-0-201-89685-5 (英語).
- Knuth, Donald. Combinatorial algorithms. The Art of Computer Programming 4A 1st. Reading, MA: Addison-Wesley Professional. 2011. ISBN 978-0-201-03804-0 (英語).
- Moffat, Alistair; Turpin, Andrew. Compression and coding algorithms. Hamburg, Germany: Kluwer Academic Publishers. 2002. ISBN 978-0-7923-7668-2. doi:10.1007/978-1-4615-0935-6 (英語).
- Sedgewick, Robert; Wayne, Kevin. Algorithms 4th. Upper Saddle River, New Jersey: Addison-Wesley Professional. 2011. ISBN 978-0-321-57351-3 (英語). Condensed web version
 ; book version
; book version  .
. - Sedgewick, Robert; Wayne, Kevin. 算法. 由謝路雲翻譯 第4版. 北京: 人民郵電出版社. 2012. ISBN 978-7-115-29380-0 (中文(中國大陸)).
- Stroustrup, Bjarne. The C++ programming language 4th. Upper Saddle River, New Jersey: Addison-Wesley Professional. 2013. ISBN 978-0-321-56384-2 (英語).
外部連結
[編輯]- Anthony Lin. Binary search algorithm (PDF). 理學維基期刊. 2019-07-02, 2 (1): 5. ISSN 2470-6345. doi:10.15347/WJS/2019.005. Wikidata Q81434400 (英語).。該論文內容取自英語維基百科的對應條目,於2018年經過外部學術同行評審。
- NIST Dictionary of Algorithms and Data Structures: binary search
- Comparisons and benchmarks of a variety of binary search implementations in C 互聯網檔案館的存檔,存檔日期2019-09-25.
























![{\displaystyle [1,2,3,4,4,5,6,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d3a10b0250aafff08cc862bc99b5f3b4f7c33f3)

![{\displaystyle [1,2,4,4,4,5,6,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5867073891e85c24ad16f2e0df8a93bd487cdec3)















![{\displaystyle [20,30,40,50,80,90,100]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2a762c441505aff6153082ad4c7863a26f52962)





















![{\displaystyle E(n)=I(n)+2n=\left[(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2\right]+2n=(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edbb46592a2cfed4a5d626d6080fd530bf7693b5)







































