相变
相变,又称物态变化

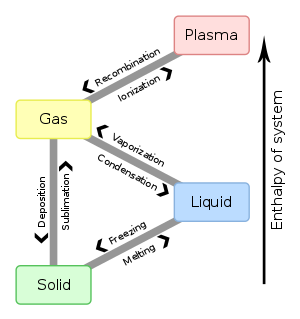
,是指物质在外部参数(如:温度、压力、磁场等等)连续变化之下,从一种相(态)忽然变成另一种相,最常见的是冰变成水和水变成蒸气。
然而,除了物体的三相变化(固态、液态、气态)自然界还存在许许多多的相变现象,例如日常生活中另一种较常见的相变是加热一块磁铁,磁铁的铁磁性忽然消失。其他在物理学中重要相变列举如下:
相变的种类
[编辑]第一个尝试将相变加以分类的是奥地利数学家、物理学家保罗·埃伦费斯特。相变分为一级相变和二级相变甚至多级相变,从数学角度讲,一级相变的热力学函数连续,但其状态函数的一阶导数不连续。二级相变的热力学函数及其关于状态函数的一阶导数都连续,但其关于状态函数的二阶导数不连续。从理论角度来看,一级相变在相变发生时,两相之间有潜热和体积等跃变。二级相变在相变发生时,两相之间无潜热和体积跃变,但有热容跃变。
相变的特性
[编辑]对称破缺
[编辑]对称性破缺(symmetry breaking)系指物理学里,在具有某种对称性的物理系统之临界点附近发生可能分岔中的一个分岔,打破了这物理系统的对称性,并且决定了这物理系统的命运。例如当水温降至接近冰点时,水中各处看起来皆相同,因此水系统具有空间上的对称性,此时若某处的温度振荡至低于冰点,便破坏了对称性,且决定了所凝固之冰的结构。对于外在观察者,不清楚有涨落(或热噪声)的存在,会觉得这选择相当随机或任意。在图样形成(pattern formation)里,对称性破缺占有重要角色。
对称性破缺可以分为两种:
明显对称性破缺:在描述物理系统的拉格朗日量或哈密顿量的数学表示里,存在明显不具有某种对称性的项。 自发对称性破缺:描述物理系统的拉格朗日量或哈密顿量具有某种对称性,但是物理系统的最低能量态(真空态)不具有此种对称性。通常,这种对称性破缺会具有一种有序参数。动力学对称性破缺是这种对称性破缺的特例。著名例子分别为标准模型中的希格斯机制、超导物理中的BCS理论。
序参量
[编辑]序参量是order parameter。
临界指数和普适类
[编辑]临界指数是指,临界点附近,定量描述物理量的临界行为时所使用的指数常数。
例子
[编辑]- 易辛模型(可以用共形场论计算临界指数)
- 别列津斯基-科斯特利茨-索利斯相变
参考文献
[编辑]- Peskin Schroeder, Quantum Field Theory
- Kardar, Statistical Theory of Fields
- Kleiner, Critical properties of phi fourth theories
- Zinn Justin, Critical phenomena