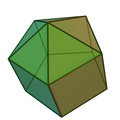
角锥柱
外观
 以五角锥柱为例 | ||
| 类别 | 棱锥柱 | |
|---|---|---|
| 对偶多面体 | 角锥柱(自身对偶) | |
| 数学表示法 | ||
| 康威表示法 | Pn+Yn | |
| 性质 | ||
| 面 | ||
| 边 | ||
| 顶点 | ||
| 欧拉特征数 | F=, E=, V= (χ=2) | |
| 组成与布局 | ||
| 面的种类 | 多边形 三角形 矩形 | |
| 对称性 | ||
| 对称群 | Cnv, [n], (*nn) | |
| 旋转对称群 | Cn, [n]+, (nn) | |
| 特性 | ||
| 凸、 demi-regular | ||
| 图像 | ||
| ||
| 注:为底面边数 。 | ||
在几何学中,角锥柱又称为棱锥柱、长锥体或长角锥(英语:Elongated pyramid),是指一系列的多面体,满足一个锥体由底面向下延伸形成柱体并与原来的锥体共同围出的一个封闭空间或一个柱体的顶面或底面其中之一各个顶点向它所在的平面外一点依次连直线段而与柱体共同为出一块封闭的空间构成,其也可以视为一个锥体与一个柱底叠在一起的几何体。由于以锥体为主,因此该系列多面体皆为自身对偶,但若底面的对偶多边形为其它形状则例外。
角锥柱系列多面体是从三开始的,因为二角锥柱已经退化成平面了。
若角锥柱的底面为正多边形则称为正角锥柱,每个面皆为正多边形的正角锥柱只有三种:正三角锥柱、正四角锥柱及正五角锥柱。
詹森多面体
[编辑]所有正角锥柱中包含了三种詹森多面体,即前面提到的三个角锥柱:正三角锥柱、正四角锥柱及正五角锥柱。
| 名称 | 面 | |
|---|---|---|
 |
正三角锥柱 (J7) | 3+1个三角形、3个正方形 |
 |
正四角锥柱 (J8) | 4个三角形、4+1个正方形 |
 |
正五角锥柱 (J9) | 5个三角形、5个正方形、1个五边形 |
参见
[编辑]参考文献
[编辑]- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller. Convex Polyhedra with Regular Faces. Consultants Bureau. 1969. No ISBN. The first proof that there are only 92 Johnson solids.
| 这是一篇与多面体相关的小作品。您可以通过编辑或修订扩充其内容。 |