辛钦常数
外观
此条目可参照英语维基百科相应条目来扩充。 |
在数论领域中,苏联数学家亚历山大·雅科夫列维奇·辛钦(Aleksandr Yakovlevich Khinchin)证明对于几乎所有实数x,其连分数表示式的系数ai的几何平均数之极限存在,且与x数值无关,此数值称为辛钦常数(英语:Khinchin's constant)。
以下是x的连分数表示式
针对任意实数x,以下的等式几乎总是为真
其中 为辛钦常数
不符合上述条件的实数包括了有理数、实系数二次方程的解(包括黄金比例 ),以及自然对数的底e。目前辛钦常数是否为无理数或代数数仍犹未可知。虽然几乎所有实数之连分数系数的几何平均都趋近于辛钦常数,但除了特意建构的实数外,并没有实数被严格证明有此性质,仅有一些数值上的证据,像是圆周率及欧拉-马歇罗尼常数。
开放问题
[编辑]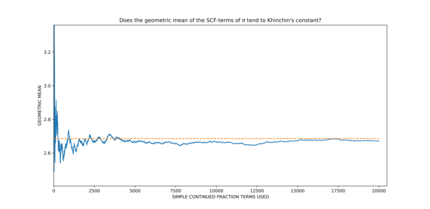
- 根据数值上的证据[1][2],圆周率π、欧拉-马斯刻若尼常数γ、以及辛钦常数本身的连分数系数ai的几何平均数会趋近辛钦常数,不过这还没有严谨的证明。
- 目前还不知道辛钦常数是有理数、代数数、无理数或超越数[3]。
相关条目
[编辑]参考资料
[编辑]- David H. Bailey, Jonathan M. Borwein, Richard E. Crandall. On the Khinchine constant (PDF). 1995. (原始内容 (PDF)存档于2005-05-28).
- Jonathan M. Borwein, David M. Bradley, Richard E. Crandall. Computational Strategies for the Riemann Zeta Function (PDF). J. Comp. App. Math. 2000, 121: p.11 [2012-11-08]. (原始内容 (PDF)存档于2006-09-25).
- Aleksandr Ya. Khinchin. Continued Fractions. New York: Dover Publications. 1997.
- Ryll-Nardzewski, Czesław, On the ergodic theorems II (Ergodic theory of continued fractions), Studia Mathematica, 1951, 12: 74–79
外部链接
[编辑]- ^ Weisstein, Eric W. Euler-Mascheroni Constant Continued Fraction. mathworld.wolfram.com. [2020-03-23]. (原始内容存档于2024-01-13) (英语).
- ^ Weisstein, Eric W. Pi Continued Fraction. mathworld.wolfram.com. [2020-03-23]. (原始内容存档于2023-11-06) (英语).
- ^ 埃里克·韦斯坦因. Khinchin's constant. MathWorld.






