介數中心性

由每個點的介數中心性從數值最低（紅色）到最高（藍色）著色的一個無向圖。

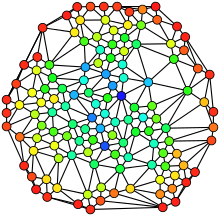
在圖論中，介數中心性（英語：betweenness centrality，又譯作中間中心性）是基於最短路徑針對網絡圖中心性的衡量標準之一。針對全連接網絡圖，其中任意兩個節點均至少存在一個最短路徑，在無權重網絡圖中該最短路徑是路徑包含邊的數量求和，加權網絡圖中該最短路徑則是路徑包含邊的權重求和。每個節點的介數中心性即為這些最短路徑穿過該節點的次數。

介數中心性在網絡理論中有廣泛的應用：它代表了某節點與其他節點之間的互動程度。 例如，在通信網絡中，一個有更高介數中心性的節點在網絡中有更強的控制能力，因為更多的信息傳遞時將通過該節點。 介數中心性被用作為對中心性的一種常見測量方式: 它適用於解決網絡理論中的許多問題，包括與社會網絡、生物、運輸和科學合作等方面相關的問題。

雖然早期的研究人員曾直觀地描述了介數的中心性，但Freeman在1977年給了第一個介數中心性的正式定義。

定義

節點$v$的介數中心性可表達為以下公式：

$g(v)=\sum _{s\neq v\neq t}{\frac {\sigma _{st}(v)}{\sigma _{st}}}$

其中$\sigma _{st}$是節點$s$到節點$t$的最短路徑之數量，而$\sigma _{st}(v)$這些路徑經過$v$的次數。

可注意到一個節點的介數中心性與該網絡圖中的節點個數相關。因此，可通過除以不包含$v$的節點對數以將計算結果標準化，使得$g\in [0,1]$。其中有向圖需除以 $(N-1)(N-2)$ ，而無向圖需除以$(N-1)(N-2)/2$，其中 $N$是網絡圖中節點數量的集合。該比例代表的是最高可能計算值，即某節點與其他所有節點都通過單一的最短路徑相連接，不過以上情況通常不會發生。標準化的過程並不會使計算的精準度受到影響。

${\mbox{normal}}(g(v))={\frac {g(v)-\min(g)}{\max(g)-\min(g)}}$

可求解得：

$\max(normal)=1$

$\min(normal)=0$

由公式可知，計算結果將始終是一個從較小範圍到更大範圍的比例，因此沒有精準度的損失。

加權網絡

在一個加權網絡中，連接節點的邊不再被看作類似於二元的互相作用（有邊或無邊），而是根據其特徵、影響、頻率等賦予對應的權重，這在網絡圖基於的網絡拓撲結構之上增加了另一個異質性的維度。 在加權網絡中，一個節點的強度為其鄰邊權重的代數和。

$s_{i}=\sum _{j=1}^{N}a_{ij}w_{ij}$

其中$a_{ij}$和$w_{ij}$分別表示節點$i$和$j$之間的鄰接矩陣和權重矩陣。類似於在無標度網絡中發現的冪律分布，一個給定節點的強度也服從冪律分布。

$s(k)\approx k^{\beta }$

一項研究表明，介數為 $b$的節點其平均值$s(b)$可用以下公式來近似：

$s(b)\approx b^{\alpha }$

滲流中心性

滲流中心性是加權介數中心性的一種特殊情況，它在計算其權重時考慮了每條最短路徑的源節點與目標節點的「狀態」。 在複雜網絡中，許多情景都會發生「感染」並進行滲流。 例如，眾所周知，在接觸網絡中細菌或病毒的感染可以在人群的社會網絡中傳播。也可以將疾病的傳播抽象化，認為一個城鎮或人群聚集地是由公路、鐵路或航空的連接而構成的網絡。計算機病毒可能通過計算機網絡傳播。關於商業報價和交易的傳聞或新聞也可以經由人群的社交網絡傳播。 在所有這些情景下，一個「感染」可在複雜網絡中通過連接傳播，並伴隨著節點「狀態」的改變，如受到感染或感染後恢復到原狀態。例如，在一個流行病的情景下，個體在感染傳播時會將狀態由「易感染」變為「已感染」。 在上述例子中，各個節點在傳播時可能的狀態可以是二元的（已受到/未受到感染）、離散的（易感染/已感染/已恢復）乃至連續的（如城鎮中受感染者的比例）。 在所有這些情景中，常見的特徵是傳染病的傳播使網絡中節點狀態發生變化。 以上這些有關滲流中心性(PC)的概念由Piraveenan et al.提出，這對具體地測量節點在網絡滲透中的重要性很有幫助。

滲流中心性的定義是：給定一個節點，在給定的時間內「滲透路徑」通過該節點的比例。「滲透路徑」指的一對節點之間的最短路徑，其中源節點產生滲透效果(例如傳播感染)，目標節點可以是處於已滲透、未滲透或部分滲透的狀態。

$PC^{t}(v)={\frac {1}{N-2}}\sum _{s\neq v\neq r}{\frac {\sigma _{sr}(v)}{\sigma _{sr}}}{\frac {{x^{t}}_{s}}{{\sum {[{x^{t}}_{i}}]}-{x^{t}}_{v}}}$

其中 $\sigma _{sr}$ 是從節點$s$到節點 $r$最短路徑數之和，$\sigma _{sr}(v)$這些路徑中通過 $v$的次數。 節點$i$在時間 $t$的滲流狀態由${x^{t}}_{i}$決定，其中有兩個臨界值，${x^{t}}_{i}=0$時表示在時間$t$的時候沒有滲透狀態，${x^{t}}_{i}=1$時表示在時間 $t$的時候為完全滲流狀態。0到1之間的值則表示部分滲透狀態（例如，在一個城鎮網絡中，這表示城鎮受感染人群的百分比）。

滲流路徑的權重取決於源節點的滲流水平，如果源節點的滲流水平越高，那麼來自該節點的路徑影響力更大。 因此在源節點為高滲透作用節點的最短路徑上的節點更有可能受到滲流影響。滲流中心性的定義還可以擴展到也包括目標節點的權重。 滲流中心性的計算可採用Brandes快速算法有效實現，其時間複雜度為$O(NM)$。如果計算需要考慮目標節點的權重，最壞情況的時間複雜度為 $O(N^{3})$。

算法

在一個網絡圖中，計算所有節點的介數中心性和接近中心性需要涉及到計算圖中所有節點對的最短路徑。如果使用改進的弗洛伊德算法需要花費$\Theta (|V|^{3})$的時間，其中需將兩點間的最短路徑修改為圖中所有節點對之間的最短路徑。 在稀疏網絡圖中，詹森算法或布蘭德斯算法效率更高，都需要花費$O(|V|^{2}\log |V|+|V||E|)$的時間。 在無權重網絡圖中，用布蘭德斯的算法計算介數中心性需要花費 $O(|V||E|)$的時間。

計算一個網絡圖所有節點的介數中心性和接近中心性時，圖是無向的且可以由環形邊（節點自己連自己）或重複邊（兩個節點多條邊）連接組成的。當專門處理網絡圖時，通常網絡圖是沒有環形邊或重複邊而只有簡單的關係（其中邊表示兩個節點之間的連接）在這種情況下，使用布蘭德斯算法計算時需要將最終結果除以2，因為每個最短路徑都被計算了兩次。

另一個算法通過引入超參數來控制探索與利用之間的平衡，從而涵蓋了可計算測地線的Freeman介數與可計算所有路徑的Newman介數。其時間複雜度為網絡圖中邊的數量乘上節點的數量。

中心性的概念也被擴展到評定一個團隊的級別。 團隊介數中心性表示通過一組節點連接非該組節點的測地線的比例。能計算所有節點介數中心性的布蘭德斯算法被修改為計算一組具有相同漸近運行時間的節點的團隊介數中心性。

相關概念

介數中心性與網絡的連接度相關，介數高的節點如果在被移除以後有很大可能性使網絡圖不完全連接。

路由介數中心性使介數中心性適用於任何循環較少的簡單路徑定義方案而不局限於最短路徑標準。

參見

• 中心性

參考文獻

• Brandes, Ulrik. A faster algorithm for betweenness centrality (PDF). Journal of Mathematical Sociology. 2001, 25 (2): 163–177 [2019-05-14]. CiteSeerX 10.1.1.11.2024 . doi:10.1080/0022250x.2001.9990249. （原始內容 (PDF)存檔於2017-10-13）. 
• Freeman, Linton. A set of measures of centrality based on betweenness. Sociometry. 1977, 40 (1): 35–41. JSTOR 3033543. doi:10.2307/3033543. 
• Goh, K. I.; Kahng, B.; Kim, D. Universal Behavior of Load Distribution in Scale-Free Networks. Physical Review Letters. 2001, 87 (27): 278701. Bibcode:2001PhRvL..87A8701G. arXiv:cond-mat/0106565 . doi:10.1103/physrevlett.87.278701. 
• Mantrach, Amin; et al. The sum-over-paths covariance kernel: A novel covariance measure between nodes of a directed graph. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2010, 32 (6): 1112–1126. doi:10.1109/tpami.2009.78. 
• Moxley, Robert L.; Moxley, Nancy F. Determining Point-Centrality in Uncontrived Social Networks. Sociometry. 1974, 37 (1): 122–130. JSTOR 2786472. doi:10.2307/2786472. 
• Newman, M. E. J. Networks: An Introduction. Oxford, UK: Oxford University Press. 2010. ISBN 978-0199206650. 
• Dolev, Shlomi; Elovici, Yuval; Puzis, Rami. Routing betweenness centrality. J. ACM. 2010, 57 (4): 25:1–25:27. doi:10.1145/1734213.1734219.