凱撒密碼
此條目需要補充更多來源。 (2022年3月27日) |
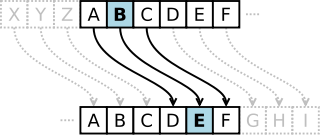 當偏移量是3的時候,所有的字母A將被替換成D,B變成E,以此類推。 | |
| 細節 | |
|---|---|
| 結構 | 替換式密碼 |
| 最佳公開破解 | |
| 易受頻率分析和暴力破解的攻擊。 | |
凱撒密碼(英語:Caesar cipher),或稱凱撒加密、凱撒變換、變換加密,是一種最簡單且最廣為人知的加密技術。凱撒密碼是一種替換加密技術,明文中的所有字母都在字母表上向後(或向前)按照一個固定數目進行偏移後被替換成密文。例如,當偏移量是3的時候,所有的字母A將被替換成D,B變成E,以此類推。這個加密方法是以羅馬共和時期凱撒的名字命名的,據稱當年凱撒曾用此方法與其將軍們進行聯繫。
凱撒密碼通常被作為其他更複雜的加密方法中的一個步驟,例如維吉尼亞密碼。凱撒密碼還在現代的ROT13系統中被應用。但是和所有的利用字母表進行替換的加密技術一樣,凱撒密碼非常容易被破解,而且在實際應用中也無法保證通信安全。
例子
[編輯]凱撒密碼的替換方法是透過排列明文和密文字母表,密文字母表示透過將明文字母表向左或向右移動一個固定數目的位置。例如,當偏移量是左移3的時候(解密時的密鑰就是3):
明文字母表:ABCDEFGHIJKLMNOPQRSTUVWXYZ 密文字母表:DEFGHIJKLMNOPQRSTUVWXYZABC
使用時,加密者查找明文字母表中需要加密的消息中的每一個字母所在位置,並且寫下密文字母表中對應的字母。需要解密的人則根據事先已知的密鑰反過來操作,得到原來的明文。例如:
明文:THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 密文:WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ
凱撒密碼的加密、解密方法還能夠透過同餘的數學方法進行計算。首先將字母用數字代替,A=0,B=1,...,Z=25。此時偏移量為n的加密方法即為:
解密就是:
歷史和用途
[編輯]
根據蘇維托尼烏斯的記載,凱撒曾用此方法對重要的軍事信息進行加密:
| “ | 如果需要保密,信中便用暗號,也即是改變字母順序,使局外人無法組成一個單詞。如果想要讀懂和理解它們的意思,得用第4個字母置換第一個字母,即以D代A,余此類推。 | ” |
| ——蘇維托尼烏斯,羅馬十二帝王傳[1] | ||
同樣,奧古斯都也使用過類似方式,只不過他是把字母向右移動一位,而且末尾不折回。
| “ | 每當他用密語寫作時,他都用B代表A,C代表B,其餘的字母也依同樣的規則;他用AA代表Z。 | ” |
| ——蘇維托尼烏斯,羅馬十二帝王傳[2] | ||
另外,有證據表明[3],凱撒曾經使用過更為複雜的密碼系統:
| “ | 文法學家普羅布斯曾經寫過一份獨具創新的手稿,研究凱撒書信中包含有秘密信息的字母。 | ” |
| ——格利烏斯,阿提卡之夜 | ||
現在已經無法弄清凱撒密碼在當時有多大的效果,但是有理由相信它是安全的。因為凱撒大部分敵人都是目不識丁的,而其餘的則可能將這些消息當作是某個未知的外語[4]。即使有某個敵人獲取了凱撒的加密信息,根據現有的記載,當時也沒有任何技術能夠解決這一最基本、最簡單的替換密碼。現存最早的破解方法記載在公元9世紀阿拉伯的阿爾·肯迪的有關發現頻率分析的著作中[5]。
特定凱撒密碼名稱
[編輯]根據偏移量的不同,還存在若干特定的凱撒密碼名稱:
- 偏移量為10:Avocat(A→K)
- 偏移量為13:ROT13
- 偏移量為-5:Cassis (K 6)
- 偏移量為-6:Cassette (K 7)
密碼破解
[編輯]即使使用唯密文攻擊,凱撒密碼也是一種非常容易破解的加密方式。可能有兩種情況需要考慮:
- 攻擊者知道(或者猜測)密碼中使用了某個簡單的替換加密方式,但是不確定是凱撒密碼;
- 攻擊者知道(或者猜測)使用了凱撒密碼,但是不知道其偏移量。
對於第一種情況,攻擊者可以透過使用諸如頻率分析或者樣式單詞分析的方法[6],馬上就能從分析結果中看出規律,得出加密者使用的是凱撒密碼。
| 偏移量 | 候選明文 |
| 0 | exxegoexsrgi |
| 1 | dwwdfndwrqfh |
| 2 | cvvcemcvqpeg |
| 3 | buubdlbupodf |
| 4 | attackatonce |
| 5 | zsszbjzsnmbd |
| 6 | yrryaiyrmlac |
| … | |
| 23 | haahjrhavujl |
| 24 | gzzgiqgzutik |
| 25 | fyyfhpfytshj |
對於第二種情況,解決方法更加簡單。由於使用凱撒密碼進行加密的語言一般都是字母文字系統,因此密碼中可能是使用的偏移量也是有限的,例如使用26個字母的英語,它的偏移量最多就是25(偏移量26等同於偏移量0,即明文;偏移量超過26,等同於偏移量1-25)。因此可以透過窮舉法,很輕易地進行破解[6]。其中一種方法是在表格中寫下密文中的某個小片段使用所有可能的偏移量解密後的內容——稱為候選明文,然後分析表格中的候選明文是否具有實際含義,得出正確的偏移量,解密整個密文。例如,被選擇出的密文片段是"EXXEGOEXSRGI",可以從右表中的候選明文里很快看出其正確的偏移量是4。也可以透過在每一個密文單詞的每一個字母下面,縱向寫下整個字母表其他字母,然後可以透過分析,得出其中的某一行便是明文。
另外一種攻擊方法是透過頻率分析。當密文長度足夠大的情況下,可以先分析密文中每個字母出現的頻率,然後將這一頻率與正常情況下的該語言字母表中所有字母的出現頻率做比較。例如在英語中,正常明文中字母E和T出現的頻率特別高,而字母Q和Z出現的頻率特別低,而在法語中出現頻率最高的字母是E,最低的是K和W。可以透過這一特點,分析密文字母出現的頻率,可以估計出正確的偏移量。此外,有時還可以將頻率分析從字母推廣到單詞,例如英語中,出現頻率最高的單詞是[7]:the, of, and, a, to, in...。透過將最常見的單詞的所有可能的25組密文,編組成字典,進行分析。比如QEB可能是the,MPQY可能是單詞know(當然也可能是aden)。但是頻率分析也有其局限性,它對於較短或故意省略元音字母或者其他縮寫方式寫成的明文加密出來的密文進行解密並不適用。
另外,透過多次使用凱撒密碼來加密並不能獲得更大的安全性,因為使用偏移量A加密得到的結果再用偏移量B加密,等同於使用A+B的偏移量進行加密的結果。


參見
[編輯]參考資料
[編輯]- ^ 蘇維托尼烏斯. 第一卷 神圣的朱里乌斯传 第56节. 罗马十二帝王传. 張竹明 王乃新 蔣平譯. 商務印書館. 1996: 30. ISBN 7100022029 (中文).
- ^ 蘇維托尼烏斯. 第二卷 神圣的奥古斯都传 第88节. 罗马十二帝王传. 張竹明 王乃新 蔣平譯. 商務印書館. 1996: 99. ISBN 7100022029 (中文).
- ^ Reinke, Edgar C. Classical Cryptography. The Classical Journal. December 1992, 58 (3): 114 (英語).
- ^ Pieprzyk, Josef; Thomas Hardjono, Jennifer Seberry. Fundamentals of Computer Security. Springer. 2003: 6. ISBN 3540431012 (英語).
- ^ 西蒙·辛格. The Code Book. Anchor. 2000: 14–20. ISBN 0385495323 (英語).
- ^ 6.0 6.1 Beutelspacher, Albrecht. Cryptology. Mathematical Association of America. 1994: 8–11. ISBN 0-88385-504-6 (英語).
- ^ The First 100 Most Commonly Used English Words. [2009-01-02]. (原始內容存檔於2013-06-16) (英語).


