熱力學系統

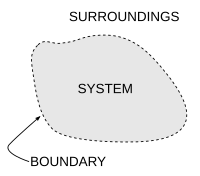
熱力學系統（英語：Thermodynamic system）是指用於熱力學研究的有限宏觀區域，是熱力學的研究對象。^[1]它的外部空間被稱為這個系統的環境。一個系統的邊界將系統與它的外部隔開。這個邊界既可以是真實存在的，也可以是假想出來的，但必須將這個系統限制在一個有限空間裡。系統與其環境可以在邊界進行物質、功、熱或其它形式能量的傳遞。而熱力學系統可以從它的邊界（或邊界的一部分）所允許的傳遞類型進行分類。

熱力學系統有一系列的狀態函數，比如體積，壓強，溫度等。這些量都是可以通過實驗測量的宏觀量。這些量的數值共同決定這個系統的熱力學狀態。一個熱力學系統的狀態函數通常存在一個或多個函數關係。這些關係可由狀態方程表述。平衡熱力學不涉及對這些狀態函數的通量的研究。因為由熱力學平衡的定義可以自然得到，這些函數的通量的值為零。當然，平衡熱力學可能會涉及使通量不為零的過程，但在熱力學過程進行前，這些過程必需停止。非平衡熱力學允許狀態函數通量不為零。通量不為零表示在系統和它的環境間存在物質，能量或熵等的傳遞。^[2]

孤立系統是一種假想存在的系統。這種系統與其外界無任何相互作用。在理想狀況下，其內部處於熱力學平衡，即它的熱力學狀態不隨時間變化。而非孤立系統根據它的邊界的性質可以與它的環境處於熱力學平衡。它們也可能處於時時變化或者循環變化（一種穩態）的非平衡狀態。系統與其環境的相互作用可以通過熱傳遞或者長程力等方式進行。

熱力學系統並非一個普遍概念，並不能代表全部的物理學系統。而這裡定義的熱力學系統的物理存在可以認為是平衡熱力學的基礎公設，儘管並沒有被列為一條熱力學定律。^[3]^[4]而在一些文獻中，熱力學第零定律通常的表述被認為是這一公設的一個推論。^[5]

熱力學系統的概念可以追溯到1824年尼古拉·卡諾對於熱機的研究。他當時稱其為熱機的工作物質。

歷史

首先發展熱力學系統這一概念是法國物理學家尼古拉·卡諾。在其於1824年發表的《論火的動力》中，他研究了熱機中的「工作物質」，例如蒸汽機中的水蒸氣。他通過這一稱法來表現這類物質在加熱時能對外做功的性質。工作物質通常與高、低溫熱源和活塞（工作物質通過推動它對外做功）接觸。1850年，德國物理學家魯道夫·克勞修斯在這一基礎上，增加了工作物質的環境的概念，並將熱力學系統稱為「做功體」。在其於1850年的一篇手記《關於火的推動力》（On the Motive Power of Fire）中，他寫道：

“

每當（做功體）的體積發生變化，氣體對外界或者外界對氣體必定要做一定量的功，這是由於氣體在膨脹時會克服外界的壓力，而其體積的收縮必須要在外界對其施加一定的壓力時才能實現。而依據我們遵從的原理，在氣體對外界或外界對氣體做這份額外的功時，必然會對應消耗或產生一定比例的額外的熱量，而氣體向「外界介質」並不能釋放與其吸收的相當的熱量。

”

邊界和環境

系統的邊界是包圍或標定熱力學系統所占據空間區域的，物質、熱量或功等等的量可以流過的，實際存在的或假想出來的二維閉合曲面。^[6]簡言之，熱力學系統的邊界是系統與環境的幾何分界。從拓撲學角度考慮, 它通常與一個二維球面同胚或分段同胚，因為熱力學系統的空間結構通常是單連通的。

系統的邊界的形狀既可以是不變的（例如一個定容反應器），也可以是可變的（例如活塞結構）。邊界既可以是真實存在的，也可以是假想出來的。對於封閉系統而言，其邊界通常是真實存在的，而開放系統的邊界通常是假想出來的。為了理論研究上的方便，系統的邊界會被設定具有絕熱，恆溫，透熱，絕緣，全透，或半透等等性質——但實際上能使邊界具有上述較為理想性質的材料可能並不存在。而邊界的體積也是可大可小的，例如它可以大到一個熱帶氣旋所占據的空間體積，也可以小到一個夸克系統所所占據的空間體積。

系統指物質世界被特別拿出研究的部分，而其環境是指在其邊界外的物質世界其它部分。依據系統的類型，系統可以與其環境發生物質、能量（包括熱量和功）、動量、電荷或其他守恆量的傳遞。除了需要考慮這些作用以外，系統的環境通常在對系統研究時會被忽略。^[7]

分類

各類熱力學系統的邊界所允許傳遞方式
熱力學系統類型	傳遞方式
	物質	功	熱
開放系統	Y	Y	Y
封閉系統	N	Y	Y
絕熱系統	N	Y	N
力學孤立系統	N	N	Y
孤立系統	N	N	N

熱力學系統依據其邊界所允許傳遞的量進行分類。

孤立系統是徹底孤立於其環境的熱力學系統。它不與其環境發生物質或能量的傳遞。而在實際情況中，徹底孤立於其環境的熱力學系統並不存在，因為系統內部與外界多少會存在一定的聯繫，比如萬有引力。

封閉系統是能與其環境傳遞能量（熱量或功）但不能傳遞物質的熱力學系統。通常溫室可以看作一個封閉系統，可以與其環境傳遞能量，不能與其環境傳遞功。一個系統與外界傳遞的是熱量或機械能或二者同時可以傳遞，通常取決於其邊界的性質。

開放系統是能與其環境傳遞能量和物質的熱力學系統。它的邊界的一部分同時允許其與環境進行物質的傳遞的性質稱為「全透性」。

力學孤立系統是指不與其環境傳遞物質或機械能，但能傳遞熱量的熱力學系統。對於一個簡單系統，力學孤立等價於其體積固定。系統中發生的過程被稱為等容過程。

絕熱系統是指不與其環境傳遞物質或熱量，但能傳遞機械能的熱力學系統。系統中發生的過程被稱為絕熱過程。

開放系統

開放系統可以通過其邊界的一些部分與外界進行物質傳遞。其邊界其它部分可能只允許能量傳遞，而並不允許物質傳遞。同時還需要考慮系統內部各部分間的能量傳遞。

流動過程

開放系統邊界所包圍的空間通常稱作控制體積。它既可以有也可以沒有實際存在的物理邊界。為了簡化研究，通常可以特別設定控制體積的形狀，這樣所有的物質流動都可以垂直於其表面進行；或者，設定過程為化學均一的物質流入或流出系統。^[8] 流入系統的物質會做功（例如被活塞推入的流體）同時，系統也可以對外做功（例如流體將活塞推出）在系統邊界不進行物質傳遞的部分，可能存在熱量 ( $δ Q$ ) 和功( $δ W$ )的傳遞，包括軸功。

經典熱力學認為如果沒有物質和能量流動，在過程起點和終點，系統都會處於內部熱平衡。而如果系統是以一致流速流動的流體，這一點依然成立。而出於簡化研究等目的，對於發生流動過程的系統，經典熱力學理論依舊可以認為是適用的。^[9]在下面的介紹中，將不考慮系統流體動能及重力勢能的變化，而系統邊界是固定並且不會發生形變。

在這些條件下，依據熱力學第一定律，我們可以得到，對於系統：系統的內能變化量等於流入系統的物質的內能加上這一過程中系統吸收熱量減去流出系統的物質的內能和系統對外做功總量。數學表達式為：

\mathrm {d} U=\mathrm {d} U_{in}+\delta Q-\mathrm {d} U_{out}-\delta W\,

其中 $U in$ 和 $U out$ 分別表示隨物質流動而流入或流出的平均內能。

於是系統就會做兩種類型的功: 如上面所示的對控制體積內流體做的「流動功」（經常也被稱為「 $PV$ 功」），和控制體積內流體對有軸承的機械做的「軸功」。這兩種類型功如下式所示：

\delta W=\mathrm {d} (P_{out}V_{out})-\mathrm {d} (P_{in}V_{in})+\delta W_{shaft}\,

代入上面描述控制體積的等式得到：

\mathrm {d} U_{cv}=\mathrm {d} U_{in}+\mathrm {d} (P_{in}V_{in})-\mathrm {d} U_{out}-\mathrm {d} (P_{out}V_{out})+\delta Q-\delta W_{shaft}\,

依據焓的定義， $H = U + PV$ ，可以將上式中內能 $U$ 和 $PV$ 功聯繫起來：

\mathrm {d} U_{cv}=\mathrm {d} H_{in}-\mathrm {d} H_{out}+\delta Q-\delta W_{shaft}\,

而如果系統在過程處於穩態，那麼系統的各屬性就不會隨時間變化。因此，系統的內能就會是個常數，也就是說上式中， $d U cv$ 等於零。這樣就可以得到一個十分有用的關係：

{\frac {\delta W_{shaft}}{\mathrm {d} t}}={\frac {\mathrm {d} H_{in}}{\mathrm {d} t}}-{\frac {\mathrm {d} H_{out}}{\mathrm {d} t}}+{\frac {\delta Q}{\mathrm {d} t}}\,

物質的選擇性傳遞

對於一個熱力學過程來說，系統的邊界和環境的屬性十分重要，因為它們決定了這一過程是否能進行。開放系統的邊界允許物質傳遞。而考慮到系統內能的變化，系統與環境的物質傳遞就需要它們進行熱能和機械能之外形式的能量的傳遞。同時這也導致了化學勢概念的產生。

當系統邊界只對某種物質全透，那麼系統就可以環境中這一物質的擴散源進行擴散式接觸，即系統就可以與環境傳遞這種物質。同時，在邊界內外同時存在那種物質的接觸平衡。通過適當的熱力學操作，物質的擴散源可以被視為一個封閉系統，其內能和熵也可以視為它的溫度、壓強和摩爾數的函數。

一些熱力學操作可以使系統邊界不允許某種物質的傳遞，而不是達到這一物質的接觸平衡，因而這就需要一個對應該物質的內含量，化學勢。對於系統某一組分 $i$ ，其化學勢記作 $μ i$ 。而這個內含量對應的外延量可以是系統中該組分的摩爾數 $N i$ 。

而對於某種物質全透的邊界內外處於接觸平衡時，其內外該物質化學勢必須相等。這是熱力學平衡性質的一部分，也可以認為與熱力學第零定律有關。^[10]

封閉系統

封閉系統不會與其環境發生物質傳遞，但系統會和其環境通過其邊界發生熱量及機械功的傳遞。一個系統與外界傳遞的是熱量或機械功或二者同時可以傳遞，通常取決於其邊界的性質。如果系統邊界絕熱，即其不允許熱量傳遞時，稱系統為絕熱系統。而當系統邊界為剛體時，即其不允許機械功傳遞時，稱系統為力學孤立系統。

壓縮衝程中的燃油-空氣混合氣體是典型的絕熱系統。而「彈式熱量計」，一種用於測定某些反應的燃燒熱的恆容熱量計，則是後者的典型例子。在其測量時，電能會從邊界流入腔體，在電極間產生電火花觸發燃燒。在燃燒後會發生熱量傳遞，但全過程不會發生物質傳遞。

關於封閉系統的熱力學過程的數學表述。首先考察熱力學第一定律對於一個開放系統的熱力學過程的表述:

\Delta U=Q-W+m_{in}(h+{\frac {1}{2}}v^{2}+gz)_{i}-m_{out}(h+{\frac {1}{2}}v^{2}+gz)_{e}

其中U是系統的內能，Q是系統吸收的熱量，W是系統對外做功，由於不會發生物質傳遞，上式中有關物質流動的部分可以忽略，由此得到熱力學第一定律對於封閉系統的表述：系統內能的變化量等於系統吸收熱量減去系統對外做功。而系統的微小變化可以表述為：

\mathrm {d} U={\delta Q}-{\delta W}.

如果系統通過在環境壓力P下體積膨脹dV方式做功，那麼W可以描述為：

{\delta W}=P\mathrm {d} V.

對於只能發生可逆過程的內部均一的系統，依據熱力學第二定律，Q可以描述為：

{\delta Q}=T\mathrm {d} S

其中T是系統的熱力學溫度，S是系統的熵。考察上述兩式，可以得到：

{\delta U}=T\mathrm {d} S-P\mathrm {d} V.

對於其中只有單一粒子（原子或分子）的簡單系統，如果它是封閉的，那麼意味著它內部的粒子數一定。然而，一個封閉系統如果內部發生化學反應，其內部的分子種類和各自的數量可能在反應過程中發生變化。而從化學反應前後的物質守恆,我們可以看出這並沒有影響其中原子（無論構成何種分子）的種類及各種原子的數量，這一點可以通過下式表現：

\sum _{j=1}^{m}a_{ij}N_{j}=b_{i}^{0}

其中N_j是j分子數量，a_ij是j中i原子的數量，b_i⁰是i原子的總量（由於系統是封閉的，其是常量）。對於各種原子，此式均成立。

孤立系統

孤立系統是與其外界沒有任何聯繫的熱力學系統。系統的邊界不允許系統與環境進行物質和能量的傳遞，其物質和能量總量不隨時間變化。孤立系統內部壓強、溫度以及物質分布會均一化。而系統所有的均一化過程最終會使系統達到熱力學平衡。

孤立系統在現實中並不存在（唯一的例外可能是宇宙整體），因為系統內部物質和外界物質間會存在像萬有引力這樣的相互作用。^[11]^[12]^[13]^[14]^[15] 然而，現實中的熱力學系統可以在一定時間內處於趨近於孤立的狀態。這時孤立系統就可以成為擬合現實世界情況的一個十分有用的模型。而在構造某些現象的數學模型時，它也是一個可以接受的理想化模型。玻爾茲曼在證明H定理（這一定理可以驗證熵增加原理）時使用了玻爾茲曼方程。而這一方程只有在系統孤立時才能嚴格成立。

熱力學平衡

熱力學系統的平衡定義為熱力學系統諸屬性不隨時間變化。通常而言，系統平衡時要比未平衡時容易研究得多。通常在研究一個熱力學過程時，可以假設每個中間過程中，系統處於平衡態。這樣可以大大簡化對於系統的研究分析。

對於可逆過程，其每一階段也必須是可逆的。而一個過程的可逆階段中，系統必須時時處於平衡。而這在現實中不能達到，只能通過使過程緩慢進行來趨近，因為過程中的每一階段在沒有打破系統平衡的前提下是不能進行的。

另見

物理學系統

參考文獻

^ 秦允豪. 《普通物理学教程热学》第三版. 高等教育出版社. 2011. ISBN 978-7-04-030090-1.
^ Eu, B.C. (2002). Generalized Thermodynamics. The Thermodynamics of Irreversible Processes and Generalized Hydrodynamics, Kluwer Academic Publishers, Dordrecht, ISBN 1-4020-0788-4.
^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 20.
^ Tisza, L. (1966). Generalized Thermodynamics, M.I.T Press, Cambridge MA, p. 119.
^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 22.
^ Perrot, Pierre. A to Z of Thermodynamics. Oxford University Press. 1998. ISBN 0-19-856552-6.
^ The Blue Book on Environment by Richard Dawkins
^ Shavit, A., Gutfinger, C. (1995). Thermodynamics. From Concepts to Applications, Prentice Hall, London, ISBN 0-13-288267-1, Chapter 6.
^ Adkins, C.J. (1968/1983). Equilibrium Thermodynamics, third edition, Cambridge University Press, Cambridge UK, ISBN 0-521-25445-0, pp. 46–47.
^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 19–23.
^ I.M.Kolesnikov; V.A.Vinokurov; S.I.Kolesnikov. Thermodynamics of Spontaneous and Non-Spontaneous Processes. Nova science Publishers. 2001: 136 [2014-01-30]. ISBN 1-56072-904-X. （原始內容存檔於2014-06-27）.
^ A System and Its Surroundings. ChemWiki. University of California - Davis. [May 2012]. （原始內容存檔於2016-02-03）.
^ Hyperphysics. The Department of Physics and Astronomy of Georgia State University. [May 2012]. （原始內容存檔於2019-01-15）.
^ Bryan Sanctuary. Open, Closed and Isolated Systems in Physical Chemistry,. Foundations of Quantum Mechanics and Physical Chemistry. McGill University (Montreal). [May 2012]. （原始內容存檔於2012-05-30）.
^ Material and Energy Balances for Engineers and Environmentalists (PDF). Imperial College Press. : 7 [May 2012]. （原始內容 (PDF)存檔於2009-08-15）.

Abbott, M.M.; van Hess, H.G. Thermodynamics with Chemical Applications 2nd. McGraw Hill. 1989.
Halliday, David; Resnick, Robert; Walker, Jearl. Fundamentals of Physics 8th. Wiley. 2008.
Moran, Michael J.; Shapiro, Howard N. Fundamentals of Engineering Thermodynamics 6th. Wiley. 2008.

外部連結

A closed system （頁面存檔備份，存於網際網路檔案館）
Thermodynamics of Systems of Constant Composition (Closed Systems) （頁面存檔備份，存於網際網路檔案館）

[普物热学-1] 秦允豪. 《普通物理学教程热学》第三版. 高等教育出版社. 2011. ISBN 978-7-04-030090-1.

[2] Eu, B.C. (2002). Generalized Thermodynamics. The Thermodynamics of Irreversible Processes and Generalized Hydrodynamics, Kluwer Academic Publishers, Dordrecht, ISBN 1-4020-0788-4.

[3] Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 20.

[4] Tisza, L. (1966). Generalized Thermodynamics, M.I.T Press, Cambridge MA, p. 119.

[5] Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 22.

[Perrot-6] Perrot, Pierre. A to Z of Thermodynamics. Oxford University Press. 1998. ISBN 0-19-856552-6.

[7] The Blue Book on Environment by Richard Dawkins

[8] Shavit, A., Gutfinger, C. (1995). Thermodynamics. From Concepts to Applications, Prentice Hall, London, ISBN 0-13-288267-1, Chapter 6.

[9] Adkins, C.J. (1968/1983). Equilibrium Thermodynamics, third edition, Cambridge University Press, Cambridge UK, ISBN 0-521-25445-0, pp. 46–47.

[10] Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 19–23.

[11] I.M.Kolesnikov; V.A.Vinokurov; S.I.Kolesnikov. Thermodynamics of Spontaneous and Non-Spontaneous Processes. Nova science Publishers. 2001: 136 [2014-01-30]. ISBN 1-56072-904-X. （原始內容存檔於2014-06-27）.

[12] A System and Its Surroundings. ChemWiki. University of California - Davis. [May 2012]. （原始內容存檔於2016-02-03）.

[13] Hyperphysics. The Department of Physics and Astronomy of Georgia State University. [May 2012]. （原始內容存檔於2019-01-15）.

[14] Bryan Sanctuary. Open, Closed and Isolated Systems in Physical Chemistry,. Foundations of Quantum Mechanics and Physical Chemistry. McGill University (Montreal). [May 2012]. （原始內容存檔於2012-05-30）.

[15] Material and Energy Balances for Engineers and Environmentalists (PDF). Imperial College Press. : 7 [May 2012]. （原始內容 (PDF)存檔於2009-08-15）.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]