在数学 中,素数计数函数 是一个用来表示小于或等于某个实数 x 的素数 的个数的函数 ,记为
π
(
x
)
{\displaystyle \pi (x)}
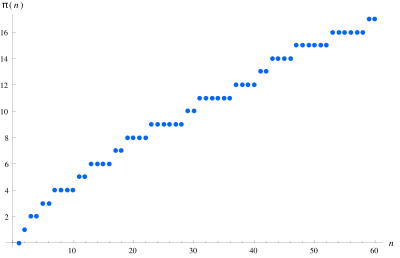
π(n )的最初60个值 在数论 中,素数计数函数的增长率 引起了很大的兴趣。在18世纪末,高斯 和勒让德 曾猜想这个函数大约为:
x
/
ln
(
x
)
{\displaystyle x/\operatorname {ln} (x)\!}
也就是
lim
x
→
∞
π
(
x
)
x
/
ln
(
x
)
=
1.
{\displaystyle \lim _{x\rightarrow \infty }{\frac {\pi (x)}{x/\operatorname {ln} (x)}}=1.\!}
这就是素数定理 。一个等价的表述,是:
lim
x
→
∞
π
(
x
)
/
li
(
x
)
=
1
{\displaystyle \lim _{x\rightarrow \infty }\pi (x)/\operatorname {li} (x)=1\!}
其中
li
(
x
)
{\displaystyle \operatorname {li} (x)}
对数积分 函数。这个定理在1896年由法国 数学家雅克·阿达马 和比利时 数学家德·拉·瓦莱布桑 先后独立给出证明 。证明用到了黎曼ζ函数 的性质。
目前已知
π
(
x
)
{\displaystyle \pi (x)\!}
π
(
x
)
=
li
(
x
)
+
O
(
x
exp
(
−
ln
(
x
)
15
)
)
{\displaystyle \pi (x)=\operatorname {li} (x)+\mathrm {O} \left(x\exp \left(-{\frac {\sqrt {\ln(x)}}{15}}\right)\right)\!}
其中O 是大O符号 。1948年,阿特勒·塞爾伯格 和保罗·埃尔德什 不使用函数或复分析 证明了素数定理。
另外一个关于素数计数函数的增长率 的猜想,是:
∑
p
≤
x
p
n
∼
π
(
x
n
+
1
)
∼
L
i
(
x
n
+
1
)
.
{\displaystyle \sum _{p\leq x}p^{n}\sim \pi (x^{n+1})\sim Li(x^{n+1}).}
x
π (x )
π (x ) − x / ln x
li(x ) − π (x )
x / π (x )
x / ln x % Error
10
4
−0.3
2.2
2.500
-7.5%
102
25
3.3
5.1
4.000
13.20%
103
168
23
10
5.952
13.69%
104
1,229
143
17
8.137
11.64%
105
9,592
906
38
10.425
9.45%
106
78,498
6,116
130
12.740
7.79%
107
664,579
44,158
339
15.047
6.64%
108
5,761,455
332,774
754
17.357
5.78%
109
50,847,534
2,592,592
1,701
19.667
5.10%
1010
455,052,511
20,758,029
3,104
21.975
4.56%
1011
4,118,054,813
169,923,159
11,588
24.283
4.13%
1012
37,607,912,018
1,416,705,193
38,263
26.590
3.77%
1013
346,065,536,839
11,992,858,452
108,971
28.896
3.47%
1014
3,204,941,750,802
102,838,308,636
314,890
31.202
3.21%
1015
29,844,570,422,669
891,604,962,452
1,052,619
33.507
2.99%
1016
279,238,341,033,925
7,804,289,844,393
3,214,632
35.812
2.79%
1017
2,623,557,157,654,233
68,883,734,693,281
7,956,589
38.116
2.63%
1018
24,739,954,287,740,860
612,483,070,893,536
21,949,555
40.420
2.48%
1019
234,057,667,276,344,607
5,481,624,169,369,960
99,877,775
42.725
2.34%
1020
2,220,819,602,560,918,840
49,347,193,044,659,701
222,744,644
45.028
2.22%
1021
21,127,269,486,018,731,928
446,579,871,578,168,707
597,394,254
47.332
2.11%
1022
201,467,286,689,315,906,290
4,060,704,006,019,620,994
1,932,355,208
49.636
2.02%
1023
1,925,320,391,606,803,968,923
37,083,513,766,578,631,309
7,250,186,216
51.939
1.93%
1024
18,435,599,767,349,200,867,866
339,996,354,713,708,049,069
17,146,907,278
54.243
1.84%
1025
176,846,309,399,143,769,411,680
3,128,516,637,843,038,351,228
55,160,980,939
56.546
1.77%
1026
1,699,246,750,872,437,141,327,603
28,883,358,936,853,188,823,261
155,891,678,121
58.850
1.70%
1027
16,352,460,426,841,680,446,427,399
267,479,615,610,131,274,163,365
508,666,658,006
61.153
1.64%
如果
x
{\displaystyle x}
π
(
x
)
{\displaystyle \pi (x)}
埃拉托斯特尼筛法 )。
一个比较复杂的计算
π
(
x
)
{\displaystyle \pi (x)}
勒让德 发现的:给定
x
{\displaystyle x}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
p
k
{\displaystyle p_{k}}
x
{\displaystyle x}
p
i
{\displaystyle p_{i}}
⌊
x
⌋
−
∑
i
⌊
x
p
i
⌋
+
∑
i
<
j
⌊
x
p
i
p
j
⌋
−
∑
i
<
j
<
k
⌊
x
p
i
p
j
p
k
⌋
+
⋯
,
{\displaystyle \lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots ,}
(其中
⌊
⋅
⌋
{\displaystyle \lfloor \cdot \rfloor }
取整函数 )。因此这个数等于:
π
(
x
)
−
π
(
x
)
+
1
{\displaystyle \pi (x)-\pi \left({\sqrt {x}}\right)+1\,}
其中
p
1
,
p
2
,
…
,
p
k
{\displaystyle p_{1},p_{2},\dots ,p_{k}}
x
{\displaystyle x}
恩斯特·梅塞尔 在1870年和1885年发表的一系列文章中,描述并使用了一个计算
π
(
x
)
{\displaystyle \pi (x)}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
p
n
{\displaystyle p_{n}}
n
{\displaystyle n}
m
{\displaystyle m}
p
i
{\displaystyle p_{i}}
Φ
(
m
,
n
)
{\displaystyle \Phi (m,n)}
Φ
(
m
,
n
)
=
Φ
(
m
,
n
−
1
)
−
Φ
(
[
m
p
n
]
,
n
−
1
)
.
{\displaystyle \Phi (m,n)=\Phi (m,n-1)-\Phi \left(\left[{\frac {m}{p_{n}}}\right],n-1\right).\,}
给定一个自然数
m
{\displaystyle m}
n
=
π
(
m
3
)
{\displaystyle n=\pi \left({\sqrt[{3}]{m}}\right)}
μ
=
π
(
m
)
−
n
{\displaystyle \mu =\pi \left({\sqrt {m}}\right)-n}
π
(
m
)
=
Φ
(
m
,
n
)
+
n
(
μ
+
1
)
+
μ
2
−
μ
2
−
1
−
∑
k
=
1
μ
π
(
m
p
n
+
k
)
.
{\displaystyle \pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right).\,}
利用这种方法,梅塞尔计算了
x
{\displaystyle x}
5 、106 、107 以及108 时
π
(
x
)
{\displaystyle \pi (x)}
1959年,德里克·亨利·勒梅尔 推广并简化了梅塞尔的方法。对于实数
m
{\displaystyle m}
n
{\displaystyle n}
k
{\displaystyle k}
P
k
(
m
,
n
)
{\displaystyle P_{k}(m,n)}
m 且正好有k 个大于
p
n
{\displaystyle p_{n}}
P
0
(
m
,
n
)
=
1
{\displaystyle P_{0}(m,n)=1}
Φ
(
m
,
n
)
=
∑
k
=
0
+
∞
P
k
(
m
,
n
)
,
{\displaystyle \Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n),\,}
这个和实际上只有有限个非零的项。设
y
{\displaystyle y}
m
3
≤
y
≤
m
{\displaystyle {\sqrt[{3}]{m}}\leq y\leq {\sqrt {m}}}
n
=
π
(
y
)
{\displaystyle n=\pi (y)}
k
{\displaystyle k}
P
1
(
m
,
n
)
=
π
(
m
)
−
n
{\displaystyle P_{1}(m,n)=\pi (m)-n}
P
k
(
m
,
n
)
=
0
{\displaystyle P_{k}(m,n)=0}
π
(
m
)
=
Φ
(
m
,
n
)
+
n
−
1
−
P
2
(
m
,
n
)
.
{\displaystyle \pi (m)=\Phi (m,n)+n-1-P_{2}(m,n).}
P
2
(
m
,
n
)
{\displaystyle P_{2}(m,n)}
P
2
(
m
,
n
)
=
∑
y
<
p
≤
m
(
π
(
m
p
)
−
π
(
p
)
+
1
)
.
{\displaystyle P_{2}(m,n)=\sum _{y<p\leq {\sqrt {m}}}\left(\pi \left({\frac {m}{p}}\right)-\pi (p)+1\right).\,}
另一方面,
Φ
(
m
,
n
)
{\displaystyle \Phi (m,n)}
Φ
(
m
,
0
)
=
⌊
m
⌋
;
{\displaystyle \Phi (m,0)=\lfloor m\rfloor ;\,}
Φ
(
m
,
b
)
=
Φ
(
m
,
b
−
1
)
−
Φ
(
m
p
b
,
b
−
1
)
.
{\displaystyle \Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right).\,}
利用这种方法,勒梅尔计算了
π
(
10
10
)
{\displaystyle \pi \left(10^{10}\right)}
我们也使用其它的素数计数函数,因为它们更方便。其中一个是黎曼的素数计数函数,通常记为
Π
0
(
x
)
{\displaystyle \Pi _{0}(x)}
p n 1/n ,而该点的值则是两边的平均值。我们可以用以下公式来定义
Π
0
(
x
)
{\displaystyle \Pi _{0}(x)}
Π
0
(
x
)
=
1
2
(
∑
p
n
<
x
1
n
+
∑
p
n
≤
x
1
n
)
{\displaystyle \Pi _{0}(x)={\frac {1}{2}}{\bigg (}\sum _{p^{n}<x}{\frac {1}{n}}\ +\sum _{p^{n}\leq x}{\frac {1}{n}}{\bigg )}}
其中p 是素数。
也可以写成以下公式:
Π
0
(
x
)
=
∑
2
x
Λ
(
n
)
ln
n
−
1
2
Λ
(
x
)
ln
x
=
∑
n
=
1
∞
1
n
π
0
(
x
1
/
n
)
{\displaystyle \Pi _{0}(x)=\sum _{2}^{x}{\frac {\Lambda (n)}{\ln n}}-{\frac {1}{2}}{\frac {\Lambda (x)}{\ln x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}(x^{1/n})}
其中Λ(n )是馮·曼戈爾特函數 ,
π
0
(
x
)
=
lim
ε
→
0
π
(
x
−
ε
)
+
π
(
x
+
ε
)
2
.
{\displaystyle \pi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )}{2}}.}
利用默比乌斯反演公式 ,可得:
π
0
(
x
)
=
∑
n
=
1
∞
μ
(
n
)
n
Π
0
(
x
1
/
n
)
{\displaystyle \pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi _{0}(x^{1/n})}
知道了黎曼ζ函数 的对数与馮·曼戈爾特函數
Λ
{\displaystyle \Lambda }
佩龙公式 ,可得:
ln
ζ
(
s
)
=
s
∫
0
∞
Π
0
(
x
)
x
−
s
+
1
d
x
{\displaystyle \ln \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s+1}\,dx}
下面是一些有用的π(x )不等式。
x
ln
x
<
π
(
x
)
<
1.25506
x
ln
x
{\displaystyle {\frac {x}{\ln x}}<\pi (x)<1.25506{\frac {x}{\ln x}}\!}
30
ln
113
113
{\displaystyle {\frac {30\ln 113}{113}}}
π
(
x
)
ln
x
x
{\displaystyle {\frac {\pi (x)\ln x}{x}}}
Pierre Dusart 在2010年证明:
x
ln
x
−
1
<
π
(
x
)
{\displaystyle {\frac {x}{\ln x-1}}<\pi (x)\!}
x
≥
5393
{\displaystyle x\geq 5393}
π
(
x
)
<
x
ln
x
−
1.1
{\displaystyle \pi (x)<{\frac {x}{\ln x-1.1}}\!}
x
≥
60184
{\displaystyle x\geq 60184}
第n 个素数p n
n
ln
n
+
n
ln
ln
n
−
n
<
p
n
<
n
ln
n
+
n
ln
ln
n
{\displaystyle n\ln n+n\ln \ln n-n<p_{n}<n\ln n+n\ln \ln n\!}
左面的不等式当n ≥ 2时成立,右面的不等式当n ≥ 6时成立,上限由Rosser(1941)提出,下限由Dusrat(1999)提出。
第n 个素数的一个估计是:
p
n
=
n
ln
n
+
n
ln
ln
n
−
n
+
n
ln
ln
n
−
2
n
ln
n
+
O
(
n
(
ln
ln
n
)
2
(
ln
n
)
2
)
.
{\displaystyle p_{n}=n\ln n+n\ln \ln n-n+{\frac {n\ln \ln n-2n}{\ln n}}+O\left({\frac {n(\ln \ln n)^{2}}{(\ln n)^{2}}}\right).}
Bach, Eric; Shallit, Jeffrey. Algorithmic Number Theory. MIT Press. 1996: volume 1 page 234 section 8.8. ISBN 0-262-02405-5 . Marc Deléglise and Jöel Rivat, Computing
π
(
x
)
{\displaystyle \pi (x)}
(页面存档备份 ,存于互联网档案馆 )Mathematics of Computation , vol. 65 , number 33, January 1996, pages 235–245 Dickson, Leonard Eugene. History of the Theory of Numbers I: Divisibility and Primality. Dover Publications. 2005. ISBN 0-486-44232-2 . Ireland, Kenneth; Rosen, Michael. A Classical Introduction to Modern Number Theory Second edition. Springer. 1998. ISBN 0-387-97329-X . Hwang H. Cheng Prime Magic conference given at the University of Bordeaux (France) at year 2001 Démarches de la Géométrie et des Nombres de l'Université du Bordeaux Titchmarsh, E. C. The Theory of Functions, 2nd ed. Oxford, England: Oxford University Press, 1960.






















![{\displaystyle \Phi (m,n)=\Phi (m,n-1)-\Phi \left(\left[{\frac {m}{p_{n}}}\right],n-1\right).\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26be5b41bb2047cd1bd449427117cd4137cda41b)
![{\displaystyle n=\pi \left({\sqrt[{3}]{m}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5f6d0fa9e23e61e64363bd63a853d4183363600)







![{\displaystyle {\sqrt[{3}]{m}}\leq y\leq {\sqrt {m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea10a085826c99b0be08340ae6a0f8aecc9bece)
























