梅森增益公式 (英語:Mason's Gain Formula ,MGF )是尋找線性信號流圖 (SFG)傳遞函數 的方法。該公式是塞繆爾·傑斐遜·梅森 [ 1] 信號流圖 確定。該方法可以很容易地處理多變量、多迴路包括內循環迴路的信號流圖。MGF經常出現在控制系統 和數字濾波器 的內容中,因為控制系統和數字濾波器常會用信號流圖表示。
增益公式如下:
G
=
y
out
y
in
=
∑
k
=
1
N
G
k
Δ
k
Δ
{\displaystyle G={\frac {y_{\text{out}}}{y_{\text{in}}}}={\frac {\sum _{k=1}^{N}{G_{k}\Delta _{k}}}{\Delta \ }}}
Δ
=
1
−
∑
L
i
+
∑
L
i
L
j
−
∑
L
i
L
j
L
k
+
⋯
+
(
−
1
)
m
∑
⋯
+
⋯
{\displaystyle \Delta =1-\sum L_{i}+\sum L_{i}L_{j}-\sum L_{i}L_{j}L_{k}+\cdots +(-1)^{m}\sum \cdots +\cdots }
其中:
Δ
{\textstyle \Delta }
y
i
n
{\displaystyle y_{\mathrm {in} }}
y
o
u
t
{\displaystyle y_{\mathrm {out} }}
G =
y
i
n
{\displaystyle y_{\mathrm {in} }}
y
o
u
t
{\displaystyle y_{\mathrm {out} }}
N =
y
i
n
{\displaystyle y_{\mathrm {in} }}
y
o
u
t
{\displaystyle y_{\mathrm {out} }}
G k
y
i
n
{\displaystyle y_{\mathrm {in} }}
y
o
u
t
{\displaystyle y_{\mathrm {out} }}
k 個前向通道的路徑增益L i L i L j L i L j L k
Δ
k
{\textstyle \Delta _{k}}
k 個前向通道的餘子式,即將接觸第 k 個前向通道的迴路增益置為0後,特徵式Δ所剩下的部分。通道:一組沿標識方向的連接輸入輸出的連續分支
前向通道:從一個輸入節點到一個輸出節點的通道,每個節點接觸不超過一次。
迴路:起始和終止在相同節點,並且沒有節點接觸兩次的通道。
路徑增益:該通道的所有分支的增益之積。
迴路增益:迴路中所有分支的增益之積[ 2] 要使用這種方法,
列出前向通道和它們的增益,將他們記為 G k
列出所有迴路和它們的增益,將他們記為 L i i 個迴路)。列出所有互不接觸的迴路和他們的增益(L i L j L i L j L k
計算特徵式 Δ 和餘子式 Δk
運用公式。
包含二端口電路的信號流圖。從輸入到輸出前向通道用不同的顏色顯示。 需要求從 Vin 到 V2 的傳遞函數。
只有一個前向通路:
Vin 到 V1 到 I2 到 V2 增益為
G
1
=
−
y
21
R
L
{\displaystyle G_{1}=-y_{21}R_{L}\,}
有三個迴路:
V1 到 I1 到 V1 增益為
L
1
=
−
R
i
n
y
11
{\displaystyle L_{1}=-R_{in}y_{11}\,}
V2 到 I2 到 V2 增益為
L
2
=
−
R
L
y
22
{\displaystyle L_{2}=-R_{L}y_{22}\,}
V1 到 I2 到 V2 到 I1 到 V1 增益為
L
3
=
y
21
R
L
y
12
R
i
n
{\displaystyle L_{3}=y_{21}R_{L}y_{12}R_{in}\,}
Δ
=
1
−
(
L
1
+
L
2
+
L
3
)
+
(
L
1
L
2
)
{\displaystyle \Delta =1-(L_{1}+L_{2}+L_{3})+(L_{1}L_{2})\,}
L1 和 L2 相互不接觸,而 L3 接觸其他兩個迴路。
Δ
1
=
1
{\displaystyle \Delta _{1}=1\,}
1 。
G
=
G
1
Δ
1
Δ
=
−
y
21
R
L
1
+
R
i
n
y
11
+
R
L
y
22
−
y
21
R
L
y
12
R
i
n
+
R
i
n
y
11
R
L
y
22
{\displaystyle G={\frac {G_{1}\Delta _{1}}{\Delta }}={\frac {-y_{21}R_{L}}{1+R_{in}y_{11}+R_{L}y_{22}-y_{21}R_{L}y_{12}R_{in}+R_{in}y_{11}R_{L}y_{22}}}\,}
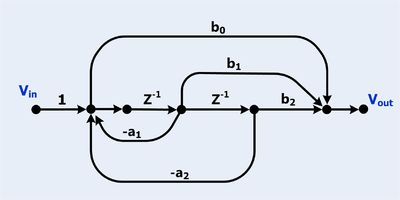
數字無限脈衝響應雙二階濾波器的信號流圖(SFG)。信號流圖有三個前向通道和兩個迴路。 經常將數字濾波器 化成信號流圖。
有兩個迴路
L
1
=
−
a
1
Z
−
1
{\displaystyle L_{1}=-a_{1}Z^{-1}\,}
L
2
=
−
a
2
Z
−
2
{\displaystyle L_{2}=-a_{2}Z^{-2}\,}
Δ
=
1
−
(
L
1
+
L
2
)
{\displaystyle \Delta =1-(L_{1}+L_{2})\,}
有三個前向通道
G
0
=
b
0
{\displaystyle G_{0}=b_{0}\,}
G
1
=
b
1
Z
−
1
{\displaystyle G_{1}=b_{1}Z^{-1}\,}
G
2
=
b
2
Z
−
2
{\displaystyle G_{2}=b_{2}Z^{-2}\,}
所有的前向通道都接觸,所以
Δ
0
=
Δ
1
=
Δ
2
=
1
{\displaystyle \Delta _{0}=\Delta _{1}=\Delta _{2}=1\,}
G
=
G
0
Δ
0
+
G
1
Δ
1
+
G
2
Δ
2
Δ
{\displaystyle G={\frac {G_{0}\Delta _{0}+G_{1}\Delta _{1}+G_{2}\Delta _{2}}{\Delta }}\,}
G
=
b
0
+
b
1
Z
−
1
+
b
2
Z
−
2
1
+
a
1
Z
−
1
+
a
2
Z
−
2
{\displaystyle G={\frac {b_{0}+b_{1}Z^{-1}+b_{2}Z^{-2}}{1+a_{1}Z^{-1}+a_{2}Z^{-2}}}\,}
伺服驅動器的信號流圖。θC = 理想的角度命令,θL = 實際負載的角度,KP = 位置迴路的增益,VωC = 速度命令, VωM = 馬達速度感測的電壓,KV =速度迴路增益,VIC = 電流命令,VIM = 電流感測器回授電壓,KC = 電流迴路增益,VA = 功率放大器輸出電壓,VM = 電感兩側的等效電壓,LM = 馬達互感,IM = 馬達電流,RM = 馬達電阻,RS = 電流感測器電阻,KM = 馬達轉矩常數(Nm/amp),T = 轉矩,M = 所有轉動元件的轉動慣量,α = 角加速度,ω = 角速度,β = 機械阻尼, GM = 馬達反電動勢常數,GT = 轉速表轉換增益常數。其中有一個前向通道(以不同顏色表示)及六個迴路。假設馬達的軸有足夠的剛性,不需視為一個彈簧。其中的常數以黑色表示,變數則以紫色表示。 此信號流中有六個迴路,分別是:
L
0
=
−
β
s
M
{\displaystyle L_{0}=-{\frac {\beta }{sM}}\,}
L
1
=
−
(
R
M
+
R
S
)
s
L
M
{\displaystyle L_{1}={\frac {-(R_{M}+R_{S})}{sL_{M}}}\,}
L
2
=
−
G
M
K
M
s
2
L
M
M
{\displaystyle L_{2}=\,{\frac {-G_{M}K_{M}}{s^{2}L_{M}M}}}
L
3
=
−
K
C
R
S
s
L
M
{\displaystyle L_{3}={\frac {-K_{C}R_{S}}{sL_{M}}}\,}
L
4
=
−
K
V
K
C
K
M
G
T
s
2
L
M
M
{\displaystyle L_{4}={\frac {-K_{V}K_{C}K_{M}G_{T}}{s^{2}L_{M}M}}\,}
L
5
=
−
K
P
K
V
K
C
K
M
s
3
L
M
M
{\displaystyle L_{5}={\frac {-K_{P}K_{V}K_{C}K_{M}}{s^{3}L_{M}M}}\,}
Δ
=
1
−
(
L
0
+
L
1
+
L
2
+
L
3
+
L
4
+
L
5
)
+
(
L
0
L
1
+
L
0
L
3
)
{\displaystyle \Delta =1-(L_{0}+L_{1}+L_{2}+L_{3}+L_{4}+L_{5})+(L_{0}L_{1}+L_{0}L_{3})\,}
只有一個前向通路:
g
0
=
−
K
P
K
V
K
C
K
M
s
3
L
M
M
{\displaystyle g_{0}={\frac {-K_{P}K_{V}K_{C}K_{M}}{s^{3}L_{M}M}}\,}
所有的前向通道都接觸,所以
Δ
0
=
1
{\displaystyle \Delta _{0}=1}
整個系統的增益是
θ
L
θ
C
=
g
0
Δ
0
Δ
{\displaystyle {\frac {\theta _{L}}{\theta _{C}}}={\frac {g_{0}\Delta _{0}}{\Delta }}\,}
梅森增益公式可以用簡單的矩陣公式表示。假設
T
{\displaystyle \mathbf {T} }
t
n
m
=
[
T
]
n
m
{\displaystyle t_{nm}=\left[\mathbf {T} \right]_{nm}}
m 到'n所有分支transmittance的和,則節點 m到'n 的增益為
u
n
m
=
[
U
]
n
m
{\displaystyle u_{nm}=\left[\mathbf {U} \right]_{nm}}
U
=
(
I
−
T
)
−
1
{\displaystyle \mathbf {U} =\left(\mathbf {I} -\mathbf {T} \right)^{-1}}
而
I
{\displaystyle \mathbf {I} }
梅森增益公式也可以用在推導有巢狀網路(其內迴路在外迴路以內)的離散網路z域傳遞函數。若是離散網路可以以信號流圖表示,則梅森增益公式可以計算網路的z域傳遞函數H(z)。
由於有向圖的路徑數會隨節點會以階乘的形式增加,因此梅森增益公式的複雜度會以階乘的形式往上成長。先考慮完整的有
n
{\displaystyle n}
y
i
n
{\displaystyle y_{in}}
y
o
u
t
{\displaystyle y_{out}}
(
n
−
2
)
!
{\displaystyle (n-2)!}
(
n
−
2
)
!
{\displaystyle (n-2)!}
高斯消去法 會比此方式有效率很多。
不過梅森增益公式將互相連接的系統的轉換函數用代數及組合的方處理,允許一些代數系統理論中較廣義的定義及計算方式。高斯消去法中會有許多的倒數計算,而梅森增益公式將其整理為單一的逆元素 ,其通式為
p
1
−
q
,
{\displaystyle {\frac {p}{1-q}},}
如上所述,
q
{\displaystyle q}
理想 。上式的分數形成有理函數 的子環
R
(
1
+
⟨
L
i
⟩
)
−
1
{\displaystyle R(1+\langle L_{i}\rangle )^{-1}}
[ 3] 里格爾公式 (Riegle's rule)所取代。
Bolton, W. Newnes. Control Engineering Pocketbook. Oxford: Newnes. 1998. Van Valkenburg, M. E. Network Analysis 3rd. Englewood Cliffs, NJ: Prentice-Hall. 1974. 



































![{\displaystyle t_{nm}=\left[\mathbf {T} \right]_{nm}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bafc8cf92f03a9ca2f0c2b992bc48f3920a57216)
![{\displaystyle u_{nm}=\left[\mathbf {U} \right]_{nm}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f97f4ff65eedb74a0f1d55973dc31a56d4ff01c)








