梅森增益公式 (英语:Mason's Gain Formula ,MGF )是寻找线性信号流图 (SFG)传递函数 的方法。该公式是塞缪尔·杰斐逊·梅森 [ 1] 信号流图 确定。该方法可以很容易地处理多变量、多回路包括内循环回路的信号流图。MGF经常出现在控制系统 和数字滤波器 的内容中,因为控制系统和数字滤波器常会用信号流图表示。
增益公式如下:
G
=
y
out
y
in
=
∑
k
=
1
N
G
k
Δ
k
Δ
{\displaystyle G={\frac {y_{\text{out}}}{y_{\text{in}}}}={\frac {\sum _{k=1}^{N}{G_{k}\Delta _{k}}}{\Delta \ }}}
Δ
=
1
−
∑
L
i
+
∑
L
i
L
j
−
∑
L
i
L
j
L
k
+
⋯
+
(
−
1
)
m
∑
⋯
+
⋯
{\displaystyle \Delta =1-\sum L_{i}+\sum L_{i}L_{j}-\sum L_{i}L_{j}L_{k}+\cdots +(-1)^{m}\sum \cdots +\cdots }
其中:
Δ
{\textstyle \Delta }
y
i
n
{\displaystyle y_{\mathrm {in} }}
y
o
u
t
{\displaystyle y_{\mathrm {out} }}
G =
y
i
n
{\displaystyle y_{\mathrm {in} }}
y
o
u
t
{\displaystyle y_{\mathrm {out} }}
N =
y
i
n
{\displaystyle y_{\mathrm {in} }}
y
o
u
t
{\displaystyle y_{\mathrm {out} }}
G k
y
i
n
{\displaystyle y_{\mathrm {in} }}
y
o
u
t
{\displaystyle y_{\mathrm {out} }}
k 个前向通道的路径增益L i L i L j L i L j L k
Δ
k
{\textstyle \Delta _{k}}
k 个前向通道的余子式,即将接触第 k 个前向通道的回路增益置为0后,特征式Δ所剩下的部分。通道:一组沿标识方向的连接输入输出的连续分支
前向通道:从一个输入节点到一个输出节点的通道,每个节点接触不超过一次。
回路:起始和终止在相同节点,并且没有节点接触两次的通道。
路径增益:该通道的所有分支的增益之积。
回路增益:回路中所有分支的增益之积[ 2] 要使用这种方法,
列出前向通道和它们的增益,将他们记为 G k
列出所有回路和它们的增益,将他们记为 L i i 个回路)。列出所有互不接触的回路和他们的增益(L i L j L i L j L k
计算特征式 Δ 和余子式 Δk
运用公式。
包含二端口电路的信号流图。从输入到输出前向通道用不同的颜色显示。 需要求从 Vin 到 V2 的传递函数。
只有一个前向通路:
Vin 到 V1 到 I2 到 V2 增益为
G
1
=
−
y
21
R
L
{\displaystyle G_{1}=-y_{21}R_{L}\,}
有三个回路:
V1 到 I1 到 V1 增益为
L
1
=
−
R
i
n
y
11
{\displaystyle L_{1}=-R_{in}y_{11}\,}
V2 到 I2 到 V2 增益为
L
2
=
−
R
L
y
22
{\displaystyle L_{2}=-R_{L}y_{22}\,}
V1 到 I2 到 V2 到 I1 到 V1 增益为
L
3
=
y
21
R
L
y
12
R
i
n
{\displaystyle L_{3}=y_{21}R_{L}y_{12}R_{in}\,}
Δ
=
1
−
(
L
1
+
L
2
+
L
3
)
+
(
L
1
L
2
)
{\displaystyle \Delta =1-(L_{1}+L_{2}+L_{3})+(L_{1}L_{2})\,}
L1 和 L2 相互不接触,而 L3 接触其他两个回路。
Δ
1
=
1
{\displaystyle \Delta _{1}=1\,}
1 。
G
=
G
1
Δ
1
Δ
=
−
y
21
R
L
1
+
R
i
n
y
11
+
R
L
y
22
−
y
21
R
L
y
12
R
i
n
+
R
i
n
y
11
R
L
y
22
{\displaystyle G={\frac {G_{1}\Delta _{1}}{\Delta }}={\frac {-y_{21}R_{L}}{1+R_{in}y_{11}+R_{L}y_{22}-y_{21}R_{L}y_{12}R_{in}+R_{in}y_{11}R_{L}y_{22}}}\,}
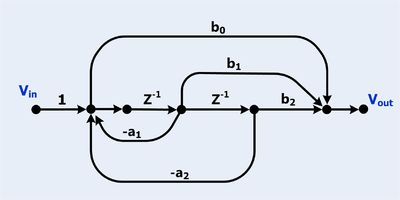
数字无限脉冲响应双二阶滤波器的信号流图(SFG)。信号流图有三个前向通道和两个回路。 经常将数字滤波器 化成信号流图。
有两个回路
L
1
=
−
a
1
Z
−
1
{\displaystyle L_{1}=-a_{1}Z^{-1}\,}
L
2
=
−
a
2
Z
−
2
{\displaystyle L_{2}=-a_{2}Z^{-2}\,}
Δ
=
1
−
(
L
1
+
L
2
)
{\displaystyle \Delta =1-(L_{1}+L_{2})\,}
有三个前向通道
G
0
=
b
0
{\displaystyle G_{0}=b_{0}\,}
G
1
=
b
1
Z
−
1
{\displaystyle G_{1}=b_{1}Z^{-1}\,}
G
2
=
b
2
Z
−
2
{\displaystyle G_{2}=b_{2}Z^{-2}\,}
所有的前向通道都接触,所以
Δ
0
=
Δ
1
=
Δ
2
=
1
{\displaystyle \Delta _{0}=\Delta _{1}=\Delta _{2}=1\,}
G
=
G
0
Δ
0
+
G
1
Δ
1
+
G
2
Δ
2
Δ
{\displaystyle G={\frac {G_{0}\Delta _{0}+G_{1}\Delta _{1}+G_{2}\Delta _{2}}{\Delta }}\,}
G
=
b
0
+
b
1
Z
−
1
+
b
2
Z
−
2
1
+
a
1
Z
−
1
+
a
2
Z
−
2
{\displaystyle G={\frac {b_{0}+b_{1}Z^{-1}+b_{2}Z^{-2}}{1+a_{1}Z^{-1}+a_{2}Z^{-2}}}\,}
伺服驱动器的信号流图。θC = 理想的角度命令,θL = 实际负载的角度,KP = 位置回路的增益,VωC = 速度命令, VωM = 马达速度感测的电压,KV =速度回路增益,VIC = 电流命令,VIM = 电流传感器回授电压,KC = 电流回路增益,VA = 功率放大器输出电压,VM = 电感两侧的等效电压,LM = 马达互感,IM = 马达电流,RM = 马达电阻,RS = 电流传感器电阻,KM = 马达转矩常数(Nm/amp),T = 转矩,M = 所有转动器件的转动惯量,α = 角加速度,ω = 角速度,β = 机械阻尼, GM = 马达反电动势常数,GT = 转速表变换增益常数。其中有一个前向通道(以不同颜色表示)及六个回路。假设马达的轴有足够的刚性,不需视为一个弹簧。其中的常数以黑色表示,变数则以紫色表示。 此信号流中有六个回路,分别是:
L
0
=
−
β
s
M
{\displaystyle L_{0}=-{\frac {\beta }{sM}}\,}
L
1
=
−
(
R
M
+
R
S
)
s
L
M
{\displaystyle L_{1}={\frac {-(R_{M}+R_{S})}{sL_{M}}}\,}
L
2
=
−
G
M
K
M
s
2
L
M
M
{\displaystyle L_{2}=\,{\frac {-G_{M}K_{M}}{s^{2}L_{M}M}}}
L
3
=
−
K
C
R
S
s
L
M
{\displaystyle L_{3}={\frac {-K_{C}R_{S}}{sL_{M}}}\,}
L
4
=
−
K
V
K
C
K
M
G
T
s
2
L
M
M
{\displaystyle L_{4}={\frac {-K_{V}K_{C}K_{M}G_{T}}{s^{2}L_{M}M}}\,}
L
5
=
−
K
P
K
V
K
C
K
M
s
3
L
M
M
{\displaystyle L_{5}={\frac {-K_{P}K_{V}K_{C}K_{M}}{s^{3}L_{M}M}}\,}
Δ
=
1
−
(
L
0
+
L
1
+
L
2
+
L
3
+
L
4
+
L
5
)
+
(
L
0
L
1
+
L
0
L
3
)
{\displaystyle \Delta =1-(L_{0}+L_{1}+L_{2}+L_{3}+L_{4}+L_{5})+(L_{0}L_{1}+L_{0}L_{3})\,}
只有一个前向通路:
g
0
=
−
K
P
K
V
K
C
K
M
s
3
L
M
M
{\displaystyle g_{0}={\frac {-K_{P}K_{V}K_{C}K_{M}}{s^{3}L_{M}M}}\,}
所有的前向通道都接触,所以
Δ
0
=
1
{\displaystyle \Delta _{0}=1}
整个系统的增益是
θ
L
θ
C
=
g
0
Δ
0
Δ
{\displaystyle {\frac {\theta _{L}}{\theta _{C}}}={\frac {g_{0}\Delta _{0}}{\Delta }}\,}
梅森增益公式可以用简单的矩阵公式表示。假设
T
{\displaystyle \mathbf {T} }
t
n
m
=
[
T
]
n
m
{\displaystyle t_{nm}=\left[\mathbf {T} \right]_{nm}}
m 到'n所有分支transmittance的和,则节点 m到'n 的增益为
u
n
m
=
[
U
]
n
m
{\displaystyle u_{nm}=\left[\mathbf {U} \right]_{nm}}
U
=
(
I
−
T
)
−
1
{\displaystyle \mathbf {U} =\left(\mathbf {I} -\mathbf {T} \right)^{-1}}
而
I
{\displaystyle \mathbf {I} }
梅森增益公式也可以用在推导有巢状网络(其内回路在外回路以内)的离散网络z域传递函数。若是离散网络可以以信号流图表示,则梅森增益公式可以计算网络的z域传递函数H(z)。
由于有向图的路径数会随节点会以阶乘的形式增加,因此梅森增益公式的复杂度会以阶乘的形式往上成长。先考虑完整的有
n
{\displaystyle n}
y
i
n
{\displaystyle y_{in}}
y
o
u
t
{\displaystyle y_{out}}
(
n
−
2
)
!
{\displaystyle (n-2)!}
(
n
−
2
)
!
{\displaystyle (n-2)!}
高斯消元法 会比此方式有效率很多。
不过梅森增益公式将互相连接的系统的变换函数用代数及组合的方处理,允许一些代数系统理论中较广义的定义及计算方式。高斯消元法中会有许多的倒数计算,而梅森增益公式将其整理为单一的逆元素 ,其通式为
p
1
−
q
,
{\displaystyle {\frac {p}{1-q}},}
如上所述,
q
{\displaystyle q}
理想 。上式的分数形成有理函数 的子环
R
(
1
+
⟨
L
i
⟩
)
−
1
{\displaystyle R(1+\langle L_{i}\rangle )^{-1}}
[ 3] 里格尔公式 (Riegle's rule)所取代。
Bolton, W. Newnes. Control Engineering Pocketbook. Oxford: Newnes. 1998. Van Valkenburg, M. E. Network Analysis 3rd. Englewood Cliffs, NJ: Prentice-Hall. 1974. 



































![{\displaystyle t_{nm}=\left[\mathbf {T} \right]_{nm}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bafc8cf92f03a9ca2f0c2b992bc48f3920a57216)
![{\displaystyle u_{nm}=\left[\mathbf {U} \right]_{nm}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f97f4ff65eedb74a0f1d55973dc31a56d4ff01c)








