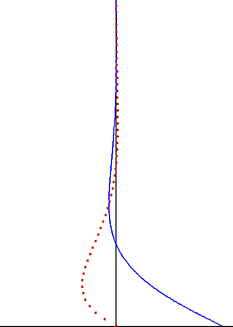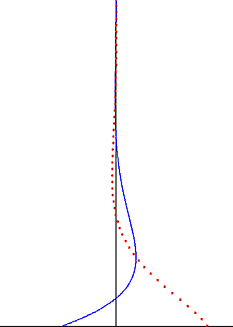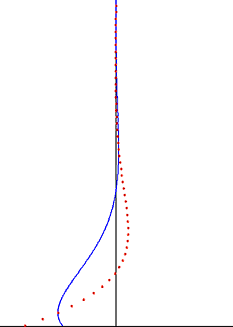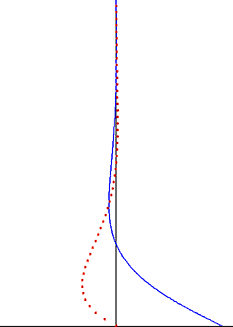
黏滯流體中受固體平面週期振盪的斯托克斯問題(底部黑色邊界)。速度(藍線)和粒子位移(紅點)為到平面距離的函數。 在流體動力學中,斯托克斯問題 (斯托克斯第二問題 ),或常稱為斯托克斯邊界層 和振盪邊界層 ,是個描述受固體平面振盪所影響的流體行為,以喬治·斯托克斯 爵士來命名。這是其中一個有精確納維-斯托克斯方程式 解的簡單非穩定問題。[ 1] [ 2] 湍流 中,這問題同樣被稱為斯托克斯邊界層,
但須仰賴實驗 數值解 近似法
考慮一個無限大平面,在
x
{\displaystyle x}
U
cos
ω
t
{\displaystyle U\cos \omega t}
y
=
0
{\displaystyle y=0}
ω
{\displaystyle \omega }
納維-斯托克斯方程式 可被簡化為
∂
u
∂
t
=
ν
∂
2
u
∂
y
2
{\displaystyle {\frac {\partial u}{\partial t}}=\nu {\frac {\partial ^{2}u}{\partial y^{2}}}}
其中
ν
{\displaystyle \nu }
運動黏度 不滑移條件
u
(
0
,
t
)
=
U
cos
ω
t
,
u
(
∞
,
t
)
=
0
,
{\displaystyle u(0,t)=U\cos \omega t,\quad u(\infty ,t)=0,}
第二個邊界條件是因為
y
=
0
{\displaystyle y=0}
因為週期性,不須考慮初始條件。因為方程式與邊界條件皆是線性的,速度函數可以寫成某個虛數函數的實數部分
u
=
U
ℜ
[
e
i
ω
t
f
(
y
)
]
{\displaystyle u=U\Re \left[e^{i\omega t}f(y)\right]}
因為
cos
ω
t
=
ℜ
e
i
ω
t
{\displaystyle \cos \omega t=\Re e^{i\omega t}}
將上式帶入偏微分方程式中,可簡化為
f
″
−
i
ω
ν
f
=
0
{\displaystyle f''-{\frac {i\omega }{\nu }}f=0}
將邊界條件帶入
f
(
0
)
=
1
,
f
(
∞
)
=
0
{\displaystyle f(0)=1,\quad f(\infty )=0}
即可得到上式方程式的解為
f
(
y
)
=
exp
[
−
1
+
i
2
ω
ν
y
]
{\displaystyle f(y)=\exp \left[-{\frac {1+i}{\sqrt {2}}}{\sqrt {\frac {\omega }{\nu }}}y\right]}
u
(
y
,
t
)
=
U
e
−
ω
2
ν
y
cos
(
ω
t
−
ω
2
ν
y
)
{\displaystyle u(y,t)=Ue^{-{\sqrt {\frac {\omega }{2\nu }}}y}\cos \left(\omega t-{\sqrt {\frac {\omega }{2\nu }}}y\right)}
受振盪平面所影響的擾動以波的形式傳播流體,但會受指數項衰減。波的滲透深度
δ
=
2
ν
/
ω
{\displaystyle \delta ={\sqrt {2\nu /\omega }}}
單位面積因流體而施加在平面上的力為
F
=
μ
(
∂
u
∂
y
)
y
=
0
=
ρ
ω
μ
U
cos
(
ω
t
−
π
4
)
{\displaystyle F=\mu \left({\frac {\partial u}{\partial y}}\right)_{y=0}={\sqrt {\rho \omega \mu }}U\cos \left(\omega t-{\frac {\pi }{4}}\right)}
在力與平面的振盪之間有產生一相位差。
振盪斯托克斯流解的一大重點是窩度 指數衰減 。[ 7] 無旋 位流 理論可用來解釋振盪運動的部分。這大大簡化了問題,也很常被應用在聲波 和水波 的無旋部分。
若流體受制於位置
y
=
h
{\displaystyle y=h}
u
(
y
,
t
)
=
U
2
(
cosh
2
λ
h
−
cos
2
λ
h
)
[
e
−
λ
(
y
−
2
h
)
cos
(
ω
t
−
λ
y
)
+
e
λ
(
y
−
2
h
)
cos
(
ω
t
+
λ
y
)
−
e
−
λ
y
cos
(
ω
t
−
λ
y
+
2
λ
h
)
−
e
λ
y
cos
(
ω
t
+
λ
y
−
2
λ
h
)
]
{\displaystyle u(y,t)={\frac {U}{2(\cosh 2\lambda h-\cos 2\lambda h)}}[e^{-\lambda (y-2h)}\cos(\omega t-\lambda y)+e^{\lambda (y-2h)}\cos(\omega t+\lambda y)-e^{-\lambda y}\cos(\omega t-\lambda y+2\lambda h)-e^{\lambda y}\cos(\omega t+\lambda y-2\lambda h)]}
其中
λ
=
ω
/
(
2
ν
)
{\displaystyle \lambda ={\sqrt {\omega /(2\nu )}}}
假設流體區域為
0
<
y
<
h
{\displaystyle 0<y<h}
y
=
h
{\displaystyle y=h}
易家訓 院士[ 8]
u
(
y
,
t
)
=
U
cos
h
/
δ
c
o
s
h
h
/
δ
2
(
cos
2
h
/
δ
+
s
i
n
h
2
h
/
δ
)
ℜ
{
W
+
W
∗
−
i
t
a
n
h
h
/
δ
tan
h
/
δ
(
W
−
W
∗
)
}
,
W
=
c
o
s
h
[
(
1
+
i
)
(
h
−
y
)
/
δ
]
e
i
ω
t
{\displaystyle u(y,t)={\frac {U\cos h/\delta \,\mathrm {cosh} \,h/\delta }{2(\cos ^{2}h/\delta +\mathrm {sinh} ^{2}h/\delta )}}\Re \left\{W+W^{*}-i\mathrm {tanh} \,h/\delta \,\tan h/\delta \,(W-W^{*})\right\},\qquad W=\mathrm {cosh} [(1+i)(h-y)/\delta ]e^{i\omega t}}
其中
δ
=
2
ν
/
ω
.
{\displaystyle \delta ={\sqrt {2\nu /\omega }}.}
受正弦曲線 遠場速度振盪影響的斯托克斯邊界層。藍縣是水平速度,紅點則是相對應的水平粒子偏移 對於振盪遠場 線性疊加原理
u
(
∞
,
t
)
=
U
∞
cos
ω
t
{\displaystyle u(\infty ,t)=U_{\infty }\cos \omega t}
u
(
0
,
t
)
=
0
{\displaystyle u(0,t)=0}
u
(
y
,
t
)
=
U
∞
[
cos
ω
t
−
e
−
ω
2
ν
y
cos
(
ω
t
−
ω
2
ν
y
)
]
,
{\displaystyle u(y,t)=U_{\infty }\left[\,\cos \omega t-{\text{e}}^{-{\sqrt {\frac {\omega }{2\nu }}}y}\,\cos \left(\omega t-{\sqrt {\frac {\omega }{2\nu }}}y\right)\right],}
在 z = 0 的地方值為0,
此與平面靜止的不滑移條件 聲波 問題碰到,或是水床附近的水波 問題。靜止平面附近的窩度振盪值與振盪平面的值相同,但差一負號。
考慮無限長、半徑為
a
{\displaystyle a}
Ω
cos
ω
t
{\displaystyle \Omega \cos \omega t}
ω
{\displaystyle \omega }
[ 9]
v
θ
=
a
Ω
ℜ
[
K
1
(
r
i
ω
/
ν
)
K
1
(
a
i
ω
/
ν
)
e
i
ω
t
]
{\displaystyle v_{\theta }=a\Omega \ \Re \left[{\frac {K_{1}(r{\sqrt {i\omega /\nu }})}{K_{1}(a{\sqrt {i\omega /\nu }})}}e^{i\omega t}\right]}
其中
K
1
{\displaystyle K_{1}}
[ 10]
v
θ
(
r
,
t
)
=
Ψ
{
[
kei
1
(
R
ω
)
kei
1
(
R
ω
r
)
+
ker
1
(
R
ω
)
ker
1
(
R
ω
r
)
]
cos
(
t
)
+
[
kei
1
(
R
ω
)
ker
1
(
R
ω
r
)
−
ker
1
(
R
ω
)
kei
1
(
R
ω
r
)
]
sin
(
t
)
}
{\displaystyle {\begin{aligned}v_{\theta }\left(r,t\right)&=\Psi \left\lbrace \left[{\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}r\right)+{\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}r\right)\right]\cos \left(t\right)\right.\\&+\left.\left[{\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}r\right)-{\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}r\right)\right]\sin \left(t\right)\right\rbrace \\\end{aligned}}}
其中
Ψ
=
[
kei
1
2
(
R
ω
)
+
ker
1
2
(
R
ω
)
]
−
1
,
{\displaystyle \Psi =\left[{\textrm {kei}}_{1}^{2}\left({\sqrt {R_{\omega }}}\right)+{\textrm {ker}}_{1}^{2}\left({\sqrt {R_{\omega }}}\right)\right]^{-1},}
k
e
i
{\displaystyle \mathrm {kei} }
k
e
r
{\displaystyle \mathrm {ker} }
開爾文函數 ,
R
ω
{\displaystyle R_{\omega }}
R
ω
=
ω
a
2
/
ν
{\displaystyle R_{\omega }=\omega a^{2}/\nu }
ν
{\displaystyle \nu }
若圓柱體在軸向以
U
cos
ω
t
{\displaystyle U\cos \omega t}
u
=
U
ℜ
[
K
0
(
r
i
ω
/
ν
)
K
0
(
a
i
ω
/
ν
)
e
i
ω
t
]
{\displaystyle u=U\ \Re \left[{\frac {K_{0}(r{\sqrt {i\omega /\nu }})}{K_{0}(a{\sqrt {i\omega /\nu }})}}e^{i\omega t}\right]}
其中
K
0
{\displaystyle K_{0}}
對於泰勒-庫埃特流 ,除了其中一個平面的平移運動,
其平面的週期運動是可以被運算的。若我們有個在
y
=
0
{\displaystyle y=0}
y
=
h
{\displaystyle y=h}
U
cos
ω
t
{\displaystyle U\cos \omega t}
u
=
U
ℜ
{
sin
k
y
sin
k
h
}
,
where
k
=
1
+
i
2
ω
ν
.
{\displaystyle u=U\ \Re \left\{{\frac {\sin ky}{\sin kh}}\right\},\quad {\text{where}}\quad k={\frac {1+i}{\sqrt {2}}}{\sqrt {\frac {\omega }{\nu }}}.}
單位面積施加在移動平面上的摩擦力為
−
μ
U
ℜ
{
k
cot
k
h
}
{\displaystyle -\mu U\Re \{k\cot kh\}}
μ
U
ℜ
{
k
csc
k
h
}
{\displaystyle \mu U\Re \{k\csc kh\}}
^ Wang, C. Y. Exact solutions of the steady-state Navier-Stokes equations. Annual Review of Fluid Mechanics. 1991, 23 : 159–177. Bibcode:1991AnRFM..23..159W doi:10.1146/annurev.fl.23.010191.001111 ^ Landau & Lifshitz (1987), pp. 83–85.
^ Batchelor, George Keith. An introduction to fluid dynamics. Cambridge university press, 2000.
^ Lagerstrom, Paco Axel. Laminar flow theory. Princeton University Press, 1996.
^ Acheson, David J. Elementary fluid dynamics. Oxford University Press, 1990.
^ Landau, Lev Davidovich, and Evgenii Mikhailovich Lifshitz. "Fluid mechanics." (1987).
^ Phillips (1977), p. 46.
^ Yih, C. S. (1968). Instability of unsteady flows or configurations Part 1. Instability of a horizontal liquid layer on an oscillating plane. Journal of Fluid Mechanics, 31(4), 737-751.
^ Drazin, Philip G. , and Norman Riley . The Navier–Stokes equations: a classification of flows and exact solutions. No. 334. Cambridge University Press, 2006.^ Rivero, M.; Garzón, F.; Núñez, J.; Figueroa, A. Study of the flow induced by circular cylinder performing torsional oscillation. European Journal of Mechanics - B/Fluids. 2019, 78 : 245–251. S2CID 201253195 doi:10.1016/j.euromechflu.2019.08.002 (英語) . ^ Landau, L. D., & Sykes, J. B. (1987). Fluid Mechanics: Vol 6. pp. 88









![{\displaystyle u=U\Re \left[e^{i\omega t}f(y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb2857823969b2e69b39aa0d3c3d4f544da6a550)



![{\displaystyle f(y)=\exp \left[-{\frac {1+i}{\sqrt {2}}}{\sqrt {\frac {\omega }{\nu }}}y\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45f9a77d8ddd35344056f57db7802abab3ab7a8c)




![{\displaystyle u(y,t)={\frac {U}{2(\cosh 2\lambda h-\cos 2\lambda h)}}[e^{-\lambda (y-2h)}\cos(\omega t-\lambda y)+e^{\lambda (y-2h)}\cos(\omega t+\lambda y)-e^{-\lambda y}\cos(\omega t-\lambda y+2\lambda h)-e^{\lambda y}\cos(\omega t+\lambda y-2\lambda h)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e44cc1792c5c6d6c2169f1e826ed40076de12f3)


![{\displaystyle u(y,t)={\frac {U\cos h/\delta \,\mathrm {cosh} \,h/\delta }{2(\cos ^{2}h/\delta +\mathrm {sinh} ^{2}h/\delta )}}\Re \left\{W+W^{*}-i\mathrm {tanh} \,h/\delta \,\tan h/\delta \,(W-W^{*})\right\},\qquad W=\mathrm {cosh} [(1+i)(h-y)/\delta ]e^{i\omega t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccaf389a956570e4c65e429bbb3a0ad46bacd3bd)



![{\displaystyle u(y,t)=U_{\infty }\left[\,\cos \omega t-{\text{e}}^{-{\sqrt {\frac {\omega }{2\nu }}}y}\,\cos \left(\omega t-{\sqrt {\frac {\omega }{2\nu }}}y\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b383f8e5e9e17b34a35daec90d3c55693d85ebb)


![{\displaystyle v_{\theta }=a\Omega \ \Re \left[{\frac {K_{1}(r{\sqrt {i\omega /\nu }})}{K_{1}(a{\sqrt {i\omega /\nu }})}}e^{i\omega t}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a127c1d08bcafa93beb50c24266bc83b6903a923)

![{\displaystyle {\begin{aligned}v_{\theta }\left(r,t\right)&=\Psi \left\lbrace \left[{\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}r\right)+{\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}r\right)\right]\cos \left(t\right)\right.\\&+\left.\left[{\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}r\right)-{\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}r\right)\right]\sin \left(t\right)\right\rbrace \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83e14063663f03df2b3655d35c7c627840f687e8)
![{\displaystyle \Psi =\left[{\textrm {kei}}_{1}^{2}\left({\sqrt {R_{\omega }}}\right)+{\textrm {ker}}_{1}^{2}\left({\sqrt {R_{\omega }}}\right)\right]^{-1},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c63f12ee316c74e344c73199f3926cd4cabcb37a)




![{\displaystyle u=U\ \Re \left[{\frac {K_{0}(r{\sqrt {i\omega /\nu }})}{K_{0}(a{\sqrt {i\omega /\nu }})}}e^{i\omega t}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275fc087cd44651ace11fe1f8428f6fc6318c7d7)



