逆变换采样

常态分布的逆变换采样

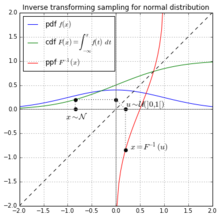
逆变换采样（英语：inverse transform sampling），又称为逆万流齐一或逆万流归宗（inversion sampling）、逆概率积分变换（inverse probability integral transform）、逆变换法（inverse transformation method）、斯米尔诺夫变换（Smirnov transform）、黄金法则（golden rule）等，是伪随机数采样的一种基本方法。在已知任意概率分布的累积分布函数时，可用于从该分布中生成随机样本。

假设$X$为一个连续随机变量，其累积分布函数为$F_{X}$。此时，随机变量$Y=F_{X}(X)$服从区间[0, 1]上的均匀分布。逆变换采样即是将该过程反过来进行：首先对于随机变量$Y$，我们从0至1中随机均匀抽取一个数$u$。之后，由于随机变量$F_{X}^{-1}(Y)$与$X$有着相同的分布，$x=F_{X}^{-1}(u)$即可看作是从分布$F_{X}$中生成的随机样本。

示例

假设有一个累积分布函数

${\begin{aligned}F(x)=1-\exp(-{\sqrt {x}}),\end{aligned}}$

我们要从该分布中生成随机样本。$F(x)$的反函数为：

${\begin{aligned}F(F^{-1}(u))&=u\\1-\exp \left(-{\sqrt {F^{-1}(u)}}\right)&=u\\F^{-1}(u)&=(-\log(1-u))^{2}\\&=(\log(1-u))^{2}.\end{aligned}}$

于是，我们先从0至1中随机均匀抽取$u$，然后计算$F^{-1}(u)=(\log(1-u))^{2}$以得到我们需要的样本。

相关条目

• 概率积分变换